[모두를 위한 딥러닝 시즌2] Lab-02 Linear regression

Linear Regression

• 학습 데이터와 가장 잘 맞는 하나의 직선을 찾는 작업

• 수학적으로 \(y = Wx + b\) 형태로 표현

• W: Weight (slope of the line)
• b: Bias (y-intercept)

W는 여러 개의 가중치를 포함하는 행렬/벡터로서, 대문자로 표기 (w1, w2…)
b는 하나의 편향 값으로, 소문자로 표기

Data definition

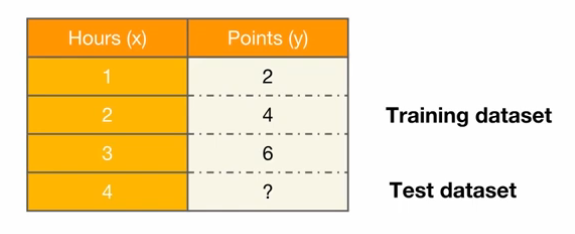
1. Training Dataset
   • 모델을 학습시키기 위한 기존 데이터
   • 입력(X)과 출력(Y)으로 구성
2. Test Dataset
   • 학습이 완료된 모델의 성능을 평가하기 위한 데이터
   • 학습에 사용되지 않은 새로운 데이터

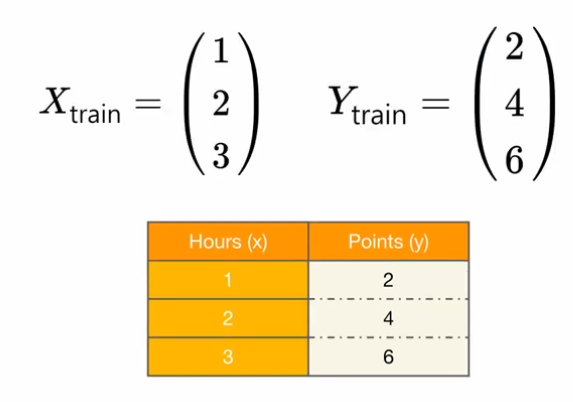
모델을 학습시키기 위한 데이터는 torch.tensor 의 형태 입력과 출력을 따로 저장

x_train = torch.FloatTensor([[1], [2], [3]]) # 입력
y_train = torch.FloatTensor([[4], [5], [6]]) # 출력

Hypothesis

\[y = W(x) + b\]

W,b의 초기화시켜서 출력을 0으로 예측

W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# W,와 b를 학습시킬 것 이라고 pytorch에 알림

Compute Loss

\[{Cost}(W, b) = \frac{1}{m} \sum_{i=1}^{m} (H(x^{(i)}) - y^{(i)})^2\]

모델이 얼마나 정답과 가까운지 나타냄
Linear Regression 에서는 MSE 함수를 이용해서 구성

cost = torch.mean((hypothesis - y_train) ** 2)

MSE를 사용하는 이유
오차의 제곱을 사용하여 양수/음수 상관없이 오차를 측정
미분 가능한 연속 함수
큰 오차에 대해 더 큰 페널티 부여

Gradient Descent

계산한 Loss를 이용하여 모델을 개선
SGD 기법 사용

optimizer = optim.SGD([W, b], lr=0.01) # 학습시킬 두 개의 데이터를 리스트로 만들어 넣음, 적당한 running rate 넣음.

optimizer.zero_grad() # zero_grad()로 gradient 초기화
cost.backward() # backward()로 gradient 계산
optimizer.step() # step() 으로 계산된 gradient 방향으로 W와 b 를 개선

SGD (Stochastic Gradient Descent) 이란?
경사 하강법의 일종으로, 전체 데이터셋이 아닌 일부 샘플(배치)을 이용하여 기울기를 계산하고 파라미터를 업데이트하는 방법

• 장점: 빠른 학습 속도, 메모리 효율성
• 단점: 불안정한 수렴 (노이즈 영향), 지역 최소값에 갇힐 수 있음

Learning Rate(lr) 이란?
Gradient Descent 과정에서 파라미터를 얼마나 업데이트할지 결정하는 상수
너무 크면 발산할 수 있고, 너무 작으면 학습이 느림

python 구현

import torch
import torch.optim as optim

torch.manual_seed(1)

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]]) # 입력
y_train = torch.FloatTensor([[2], [4], [6]]) # 출력

# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# W,와 b를 학습시킬 것 이라고 pytorch에 알림

# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.01) # 학습시킬 두 개의 데이터를 리스트로 만들어 넣음, 적당한 running rate 넣음.

nb_epochs = 1000
for epoch in range(nb_epochs + 1):
    
    # H(x) 계산
    hypothesis = x_train * W + b
    
    # cost 계산
    cost = torch.mean((hypothesis - y_train) ** 2)

    # cost로 H(x) 개선
    optimizer.zero_grad() # zero_grad()로 gradient 초기화
    cost.backward() # backward()로 gradient 계산
    optimizer.step() # step() 으로 계산된 gradient 방향으로 W와 b 를 개선

    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
            epoch, nb_epochs, W.item(), b.item(), cost.item()
        ))
        # Epoch    0/1000 W: 0.187, b: 0.080 Cost: 18.666666
        # Epoch  100/1000 W: 1.746, b: 0.578 Cost: 0.048171
        # Epoch  200/1000 W: 1.800, b: 0.454 Cost: 0.029767
        # Epoch  300/1000 W: 1.843, b: 0.357 Cost: 0.018394
        # Epoch  400/1000 W: 1.876, b: 0.281 Cost: 0.011366
        # Epoch  500/1000 W: 1.903, b: 0.221 Cost: 0.007024
        # Epoch  600/1000 W: 1.924, b: 0.174 Cost: 0.004340
        # Epoch  700/1000 W: 1.940, b: 0.136 Cost: 0.002682
        # Epoch  800/1000 W: 1.953, b: 0.107 Cost: 0.001657
        # Epoch  900/1000 W: 1.963, b: 0.084 Cost: 0.001024
        # Epoch 1000/1000 W: 1.971, b: 0.066 Cost: 0.000633

심화 : nn.Module