[모두를 위한 딥러닝 시즌2] Lab-03 Deeper Look at GD

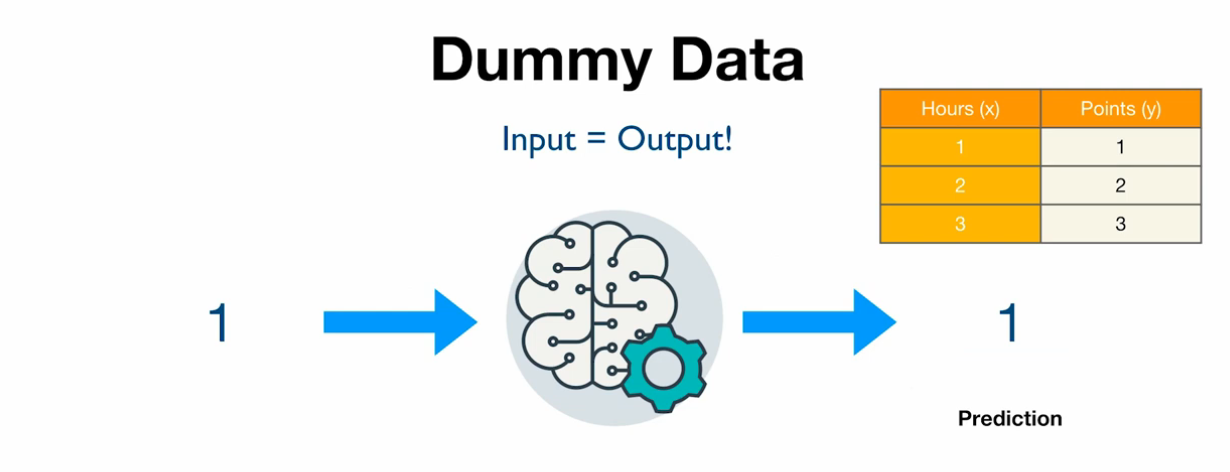
Simpler Hypothesis Function

\[y = W(x)\]

편향(bias) b를 제외한 단순한 형태로 구성된 모델

이 모델은 실제 데이터에서는 사용하기에 부족하지만, 기초적인 선형 회귀의 개념을 학습하기에 적합

x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])

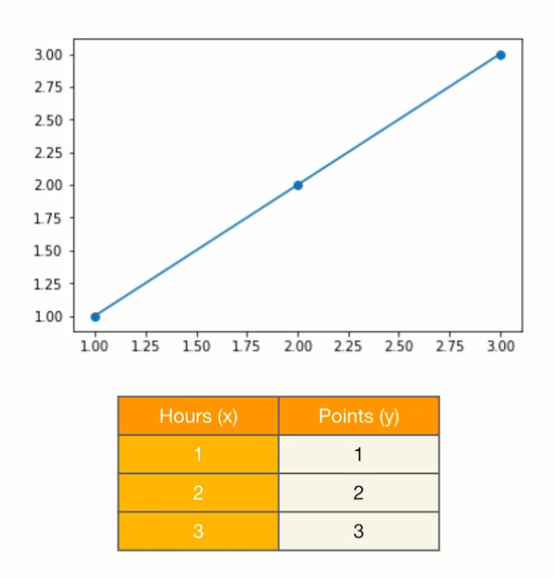
위의 데이터셋에서는 H(x) = x가 정확한 모델이며, W = 1이 가장 적합한 가중치

Cost Funtion

모델의 좋고 나쁨을 평가하는 방법

모델의 예측값이 실제데이터와 얼마나 다른지 나타냄
잘 학습될 모델일수록 낮은 코스트를 가짐

\[\frac{\partial \text{cost}}{\partial W} = \nabla W\]

Linear Regression에서는 보통 Mean Squared Error를 cost function으로 사용함

Gradient Descent

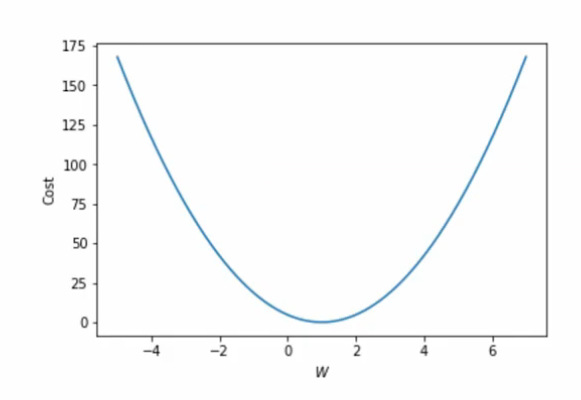
Cost(W)를 최소화하기 위해 Gradient(기울기)를 계산하여, W 값을 업데이트

• 기울기(gradient)가 음수일 경우: W 값을 증가
• 기울기(gradient)가 양수일 경우: W 값을 감소

\[\text{cost}(W) = \frac{1}{m} \sum_{i=1}^{m} \left(Wx^{(i)} - y^{(i)}\right)^2\] \[\nabla W = \frac{\partial \text{cost}}{\partial W} = \frac{2}{m} \sum_{i=1}^{m} \left(Wx^{(i)} - y^{(i)}\right)x^{(i)}\] \[W := W - \alpha \nabla W\]

:=는 할당(assign)을 나타내는 기호
\(W\) 를 \(W - \alpha \nabla W\) 로 업데이트한다는 의미

python 구현

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
W = torch.zeros(1)
# learning rate 설정
lr = 0.1

nb_epochs = 10
for epoch in range(nb_epochs + 1):
    
    # H(x) 계산
    hypothesis = x_train * W
    
    # cost gradient 계산
    cost = torch.mean((hypothesis - y_train) ** 2)
    gradient = torch.sum((W * x_train - y_train) * x_train)

    print('Epoch {:4d}/{} W: {:.3f}, Cost: {:.6f}'.format(
        epoch, nb_epochs, W.item(), cost.item()
    ))

    # cost gradient로 H(x) 개선
    W -= lr * gradient

# Epoch    0/10 W: 0.000, Cost: 4.666667
# Epoch    1/10 W: 1.400, Cost: 0.746666
# Epoch    2/10 W: 0.840, Cost: 0.119467
# Epoch    3/10 W: 1.064, Cost: 0.019115
# Epoch    4/10 W: 0.974, Cost: 0.003058
# Epoch    5/10 W: 1.010, Cost: 0.000489
# Epoch    6/10 W: 0.996, Cost: 0.000078
# Epoch    7/10 W: 1.002, Cost: 0.000013
# Epoch    8/10 W: 0.999, Cost: 0.000002
# Epoch    9/10 W: 1.000, Cost: 0.000000
# Epoch   10/10 W: 1.000, Cost: 0.000000

torch.optim

PyTorch에서는 Gradient Descent를 쉽게 구현하기 위해 torch.optim 모듈을 제공

주요 단계

1. 시작할 때 Optimizer 정의
2. optimizer.zero_grad()로 Gradient를 0으로 초기화
3. cost.backward()로 Gradient 계산
4. optimizer.step()으로 W를 Gradient 방향으로 업데이트

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W], lr=0.15)

nb_epochs = 10
for epoch in range(nb_epochs + 1):
    
    # H(x) 계산
    hypothesis = x_train * W
    
    # cost 계산
    cost = torch.mean((hypothesis - y_train) ** 2)

    print('Epoch {:4d}/{} W: {:.3f} Cost: {:.6f}'.format(
        epoch, nb_epochs, W.item(), cost.item()
    ))

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

# Epoch    0/10 W: 0.000 Cost: 4.666667
# Epoch    1/10 W: 1.400 Cost: 0.746667
# Epoch    2/10 W: 0.840 Cost: 0.119467
# Epoch    3/10 W: 1.064 Cost: 0.019115
# Epoch    4/10 W: 0.974 Cost: 0.003058
# Epoch    5/10 W: 1.010 Cost: 0.000489
# Epoch    6/10 W: 0.996 Cost: 0.000078
# Epoch    7/10 W: 1.002 Cost: 0.000013
# Epoch    8/10 W: 0.999 Cost: 0.000002
# Epoch    9/10 W: 1.000 Cost: 0.000000
# Epoch   10/10 W: 1.000 Cost: 0.000000

torch.optim 모듈은 다양한 최적화 알고리즘(SGD, Adam, RMSProp 등)을 제공하여 보다 편리한 학습 과정 설정 가능

전체 코드

import torch
import torch.optim as optim

torch.manual_seed(1)

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])

# 모델 초기화
# W = torch.zeros(1)
# learning rate 설정
# lr = 0.1

# 모델 초기화
W = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W], lr=0.15)

nb_epochs = 10
for epoch in range(nb_epochs + 1):
    
    # H(x) 계산
    hypothesis = x_train * W
    
    # cost gradient 계산
    # cost = torch.mean((hypothesis - y_train) ** 2)
    # gradient = torch.sum((W * x_train - y_train) * x_train)

    # cost 계산
    cost = torch.mean((hypothesis - y_train) ** 2)

    print('Epoch {:4d}/{} W: {:.3f}, Cost: {:.6f}'.format(
        epoch, nb_epochs, W.item(), cost.item()
    ))
    # Epoch    0/10 W: 0.000, Cost: 4.666667  
    # Epoch    1/10 W: 1.400, Cost: 0.746666
    # Epoch    2/10 W: 0.840, Cost: 0.119467
    # Epoch    3/10 W: 1.064, Cost: 0.019115
    # Epoch    4/10 W: 0.974, Cost: 0.003058
    # Epoch    5/10 W: 1.010, Cost: 0.000489
    # Epoch    6/10 W: 0.996, Cost: 0.000078
    # Epoch    7/10 W: 1.002, Cost: 0.000013
    # Epoch    8/10 W: 0.999, Cost: 0.000002
    # Epoch    9/10 W: 1.000, Cost: 0.000000
    # Epoch   10/10 W: 1.000, Cost: 0.000000

    # cost gradient로 H(x) 개선
    # W -= lr * gradient

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()