[모두를 위한 딥러닝 시즌2] Lab-04-1 Multivariable Linear regression

Multivariate Linear Regression

Simpler Linear Regression

• 하나의 정보로부터 하나의 결론을 예측

but, 대부분 경우 예측을 위해서는 더욱 다양한 정보가 필요

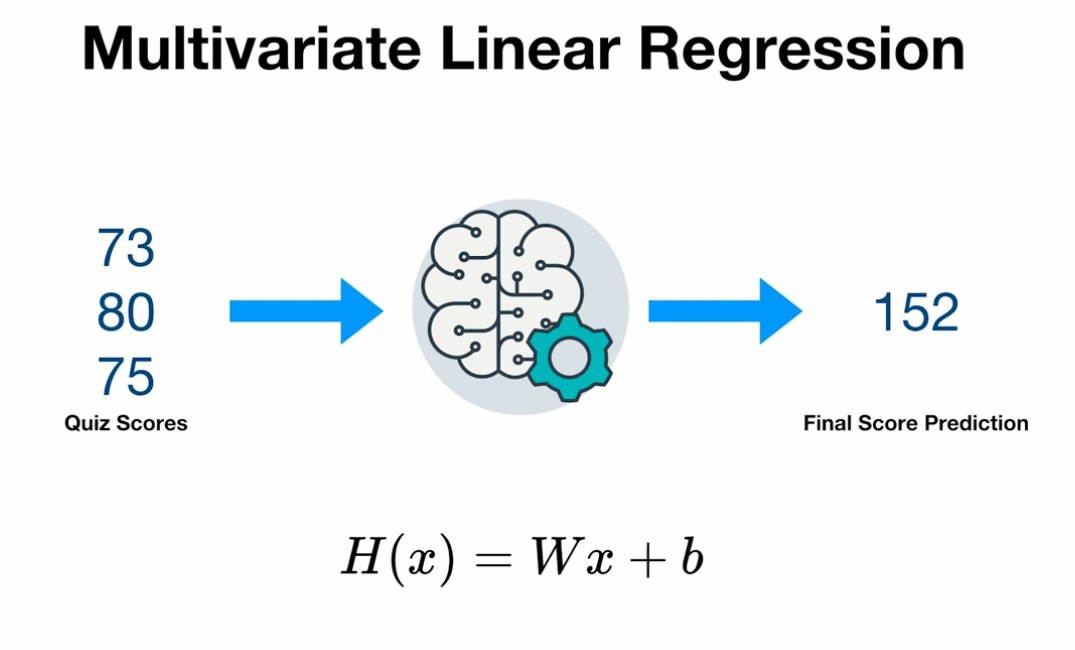
복수의 정보를 통해 하나의 추측값을 계산
(예: 쪽지시험 성적 73,80,75 점인 학생의 기말고사 성적 예측)

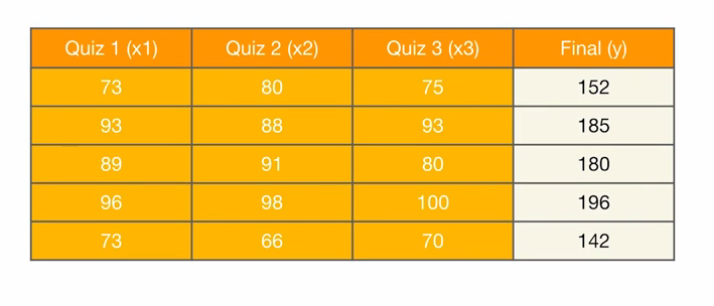
Data

x_train = torch.FloatTensor([[73, 80, 75], 
                             [93, 88, 93],
                             [89, 91, 90],
                             [96, 98, 100],
                             [73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], 142])

Hypothesis Function

\[H(x) = Wx + b\]

vector x 와 matrix W 곱

\[H(x) = w_1 x_1 + w_2 x_2 + w_3 x_3 + b\]

입력변수 x가 3개라면 weight도 3개

# H(x) 계산 1
hypothesis = x1_train * w1 + x2_train * w2 + x3_train * w3 + b

# 하지만 x 길이가 1000이라면? 
# matmul() 을 이용하여 계산

# H(x) 계산 2
hypothesis = x_train.matmul(W) + b # or .mm or @
# mm = 2차원 텐서에만 사용할 수 있는 행렬 곱셈 메서드
# @ = Python의 행렬 곱셈 연산자(@)

matmul()은 벡터화(Vectorization), GPU 가속 및 최적화, 메모리 접근 패턴 최적화등을 통해 빠른 연산이 가능

Cost Funtion

\[\text{cost}(W) = \frac{1}{m} \sum_{i=1}^{m} \left(Wx^{(i)} - y^{(i)}\right)^2\]

기존 Simple Linear Regression과 동일한 MSE 사용

cost = torch.mean((hypothesis - y_train) ** 2)

Gradient Descent with torch.optim

\[\nabla W = \frac{\partial \text{cost}}{\partial W} = \frac{2}{m} \sum_{i=1}^{m} \left(Wx^{(i)} - y^{(i)}\right)x^{(i)}\] \[W := W - \alpha \nabla W\]

기존 Simple Linear Regression과 동일한 학습 방식

# 데이터
x_train = torch.FloatTensor([[73, 80, 75],
                             [93, 88, 93],
                             [89, 91, 90],
                             [96, 98, 100],
                             [73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])

# 모델 초기화
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

# optimizer 설정
optimizer = optim.SGD([W, b], lr=1e-5)

nb_epochs = 20
for epoch in range(nb_epochs + 1):
    
    # H(x) 계산
    hypothesis = x_train.matmul(W) + b # or .mm or @

    # cost 계산
    cost = torch.mean((hypothesis - y_train) ** 2)

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    # 100번마다 로그 출력
    print('Epoch {:4d}/{} hypothesis: {} Cost: {:.6f}'.format(
        epoch, nb_epochs, hypothesis.squeeze().detach(), cost.item()
    ))

# % Epoch    0/20 hypothesis: tensor([0., 0., 0., 0., 0.]) Cost: 29661.800781
# % Epoch    1/20 hypothesis: tensor([67.2578, 80.8397, 79.6523, 86.7394, 61.6605]) Cost: 9298.520508
# % Epoch    2/20 hypothesis: tensor([104.9128, 126.0990, 124.2466, 135.3015,  96.1821]) Cost: 2915.713135
# % Epoch    3/20 hypothesis: tensor([125.9942, 151.4381, 149.2133, 162.4896, 115.5097]) Cost: 915.040527
# % Epoch    4/20 hypothesis: tensor([137.7968, 165.6247, 163.1911, 177.7112, 126.3307]) Cost: 287.936005
# % Epoch    5/20 hypothesis: tensor([144.4044, 173.5674, 171.0168, 186.2332, 132.3891]) Cost: 91.371017
# % Epoch    6/20 hypothesis: tensor([148.1035, 178.0144, 175.3980, 191.0042, 135.7812]) Cost: 29.758139
# % Epoch    7/20 hypothesis: tensor([150.1744, 180.5042, 177.8508, 193.6753, 137.6805]) Cost: 10.445305
# % Epoch    8/20 hypothesis: tensor([151.3336, 181.8983, 179.2240, 195.1707, 138.7440]) Cost: 4.391228
# % Epoch    9/20 hypothesis: tensor([151.9824, 182.6789, 179.9928, 196.0079, 139.3396]) Cost: 2.493135
# % Epoch   10/20 hypothesis: tensor([152.3454, 183.1161, 180.4231, 196.4765, 139.6732]) Cost: 1.897688
# % Epoch   11/20 hypothesis: tensor([152.5485, 183.3610, 180.6640, 196.7389, 139.8602]) Cost: 1.710541
# % Epoch   12/20 hypothesis: tensor([152.6620, 183.4982, 180.7988, 196.8857, 139.9651]) Cost: 1.651413
# % Epoch   13/20 hypothesis: tensor([152.7253, 183.5752, 180.8742, 196.9678, 140.0240]) Cost: 1.632387
# % Epoch   14/20 hypothesis: tensor([152.7606, 183.6184, 180.9164, 197.0138, 140.0571]) Cost: 1.625923
# % Epoch   15/20 hypothesis: tensor([152.7802, 183.6427, 180.9399, 197.0395, 140.0759]) Cost: 1.623412
# % Epoch   16/20 hypothesis: tensor([152.7909, 183.6565, 180.9530, 197.0538, 140.0865]) Cost: 1.622141
# % Epoch   17/20 hypothesis: tensor([152.7968, 183.6643, 180.9603, 197.0618, 140.0927]) Cost: 1.621253
# % Epoch   18/20 hypothesis: tensor([152.7999, 183.6688, 180.9644, 197.0662, 140.0963]) Cost: 1.620500
# % Epoch   19/20 hypothesis: tensor([152.8014, 183.6715, 180.9666, 197.0686, 140.0985]) Cost: 1.619770
# % Epoch   20/20 hypothesis: tensor([152.8020, 183.6731, 180.9677, 197.0699, 140.1000]) Cost: 1.619033

lr 설정 큰 값에서 작은 값으로 조정
1e-4 ~ 1e-6 : 긴 학습 주기 동안 매우 안정적이고 천천히 학습할 수 있는 값 (1000)
1e-3 ~ 1e-5 : 학습이 안정적으로 이루어지면서도 적당한 속도로 수렴 (500 ~ 1000)
1e-2 ~ 1e-4 : 초기 학습이 빠르게 이루어져야 하는 경우 (100 ~ 500)
1e-1 ~ 1e-3 : 학습 속도를 극대화 (100이하)

nn.Module

W와 b를 일일히 선언하는건 모델이 커질수록 귀찮은 일

# 모델 초기화
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True) 

hypothesis = x_train.matmul(W) + b # or .mm or @

pytorch에서 nn.Module을 이용해 편하게 가능

1. nn.Module을 상속해서 모델 생성
2. nnLinear(3, 1)
   • 입력 차원: 3
   • 출력 차원: 1
3. Hypothesis 계산은 forward()
4. Gradient 계산은 backword()

import torch.nn as nn

class MultivariateLinearRegressionModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(3, 1)

    def forward(self, x):
        return self.linear(x)

hypothesis = model(x_train)

forward(): 순전파(Forward Propagation) 과정을 정의하여 입력 데이터를 변환하고 출력을 계산
backward(): 역전파(Backward Propagation) 과정으로 손실을 기준으로 각 파라미터의 변화도를 자동으로 계산
자동 미분(Autograd)을 통해 backward()는 별도로 구현할 필요 없이 cost.backward()로 변화도 계산 가능
ref: https://tutorials.pytorch.kr/beginner/blitz/autograd_tutorial.html

F.mse_loss

pytorch에서는 다양한 cost function을 제공

• 다른 cost function으로 변경 시 편리
• cost function 계산 오류 방지

import torch.nn.functional as F

# 기존 cost function
cost = torch.mean((hypothesis - y_train) ** 2)

# pytorch cost function
cost = F.mse_loss(prediction, y_train)

hypothesis vs prediction
hypothesis: 직접 수식을 사용하여 계산
prediction: 모델 클래스를 사용하여 예측
prediction를 이용하면 자동 미분(autograd)과 레이어 관리가 수월

pytorch module 적용

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

torch.manual_seed(1)

class MultivariateLinearRegressionModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(3, 1)

    def forward(self, x):
        return self.linear(x)

# 데이터
x_train = torch.FloatTensor([[73, 80, 75],
                             [93, 88, 93],
                             [89, 91, 90],
                             [96, 98, 100],
                             [73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])


# 모델 초기화
# W = torch.zeros((3, 1), requires_grad=True)
# b = torch.zeros(1, requires_grad=True)
model = MultivariateLinearRegressionModel()

hypothesis = model(x_train)

# optimizer 설정
# optimizer = optim.SGD([W, b], lr=1e-5)
optimizer = optim.SGD(model.parameters(), lr=1e-5)

nb_epochs = 20
for epoch in range(nb_epochs + 1):
    
    # H(x) 계산 1
    # hypothesis = x1_train * w1 + x2_train * w2 + x3_train * w3 + b

    # 하지만 x 길이가 1000이라면? 
    # matmul() 을 이용하여 계산

    # H(x) 계산 2
    # hypothesis = x_train.matmul(W) + b # or .mm or @
    prediction = model(x_train)

    # cost 계산
    # cost = torch.mean((hypothesis - y_train) ** 2)
    cost = F.mse_loss(prediction, y_train)

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    # 20번마다 로그 출력
    print('Epoch {:4d}/{} Cost: {:.6f}'.format(
        epoch, nb_epochs, cost.item()
    ))
    # Epoch    0/20 Cost: 31667.597656
    # Epoch    1/20 Cost: 9926.266602
    # Epoch    2/20 Cost: 3111.513916
    # Epoch    3/20 Cost: 975.451599
    # Epoch    4/20 Cost: 305.908691
    # Epoch    5/20 Cost: 96.042679
    # Epoch    6/20 Cost: 30.260746
    # Epoch    7/20 Cost: 9.641718
    # Epoch    8/20 Cost: 3.178694
    # Epoch    9/20 Cost: 1.152871
    # Epoch   10/20 Cost: 0.517863
    # Epoch   11/20 Cost: 0.318801
    # Epoch   12/20 Cost: 0.256388
    # Epoch   13/20 Cost: 0.236816
    # Epoch   14/20 Cost: 0.230660
    # Epoch   15/20 Cost: 0.228719
    # Epoch   16/20 Cost: 0.228095
    # Epoch   17/20 Cost: 0.227881
    # Epoch   18/20 Cost: 0.227802
    # Epoch   19/20 Cost: 0.227760
    # Epoch   20/20 Cost: 0.227729