[모두를 위한 딥러닝 시즌2] Lab-05 Logistic Regression
[모두를 위한 딥러닝 시즌2] Lab-05 Logistic Regression
Logistic Regression 이란 ?
이진 분류(binary classification) 문제
- 데이터는 여러 개의 특징(feature)으로 이루어짐 (환자의 키, 몸무게, 나이와 같은 정보
- 이 데이터가 결과적으로 1인지 0인지(참/거짓)를 예측
- 스팸 메일인지 아닌지를 구분
- 환자가 특정 질병에 걸렸는지 여부를 예측
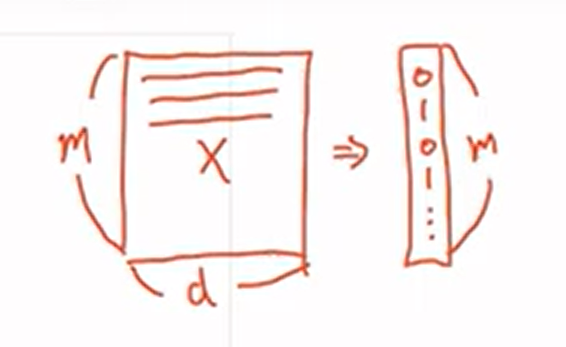
m개의 샘플, d의 dim을 가진 데이터 x 가 주어지면
m개의 0과 1로 이루어진 예측값을 출력함
이때 x의 어떤 값이 1일 확률
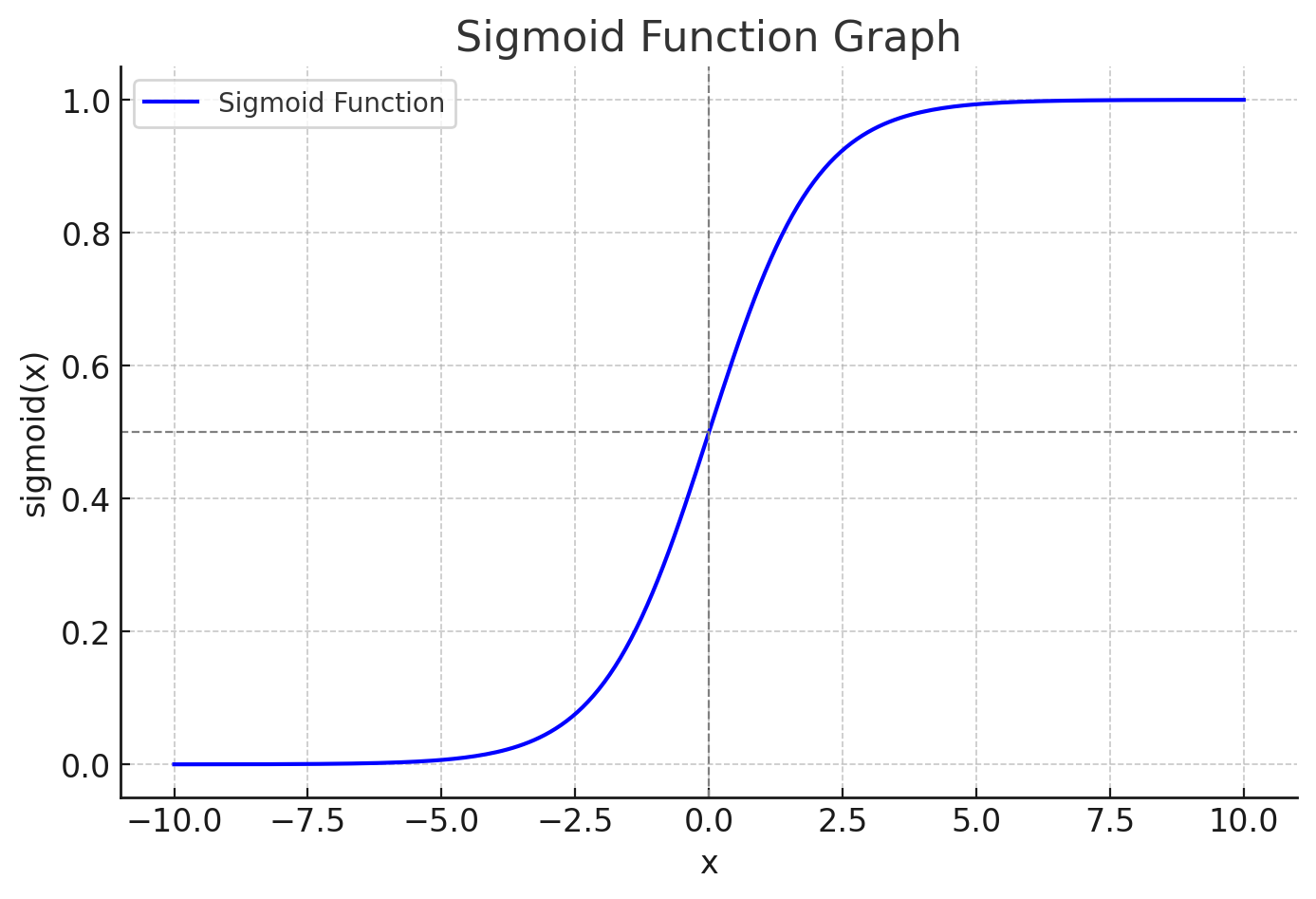
\[P(x=1) = 1-P(x=0)\]Hypothesis : 주어진 특징들의 선형 결합(즉, 일종의 합)을 시그모이드 함수로 변환한 결과
\[H(X) = \frac{1}{1 + e^{-w^T X}}\]Sigmoid 함수 $\sigma(x) = \frac{1}{1 + e^{-x}}$ 를 사용하여 cost 함수를 정의
\[cost(W) = -\frac{1}{m} \sum y \log(H(x)) + (1 - y) \log(1 - H(x))\]이 코스트 함수를 $cost(W) = \frac{1}{m} \sum c(H(x), y)$ 로 나타내면
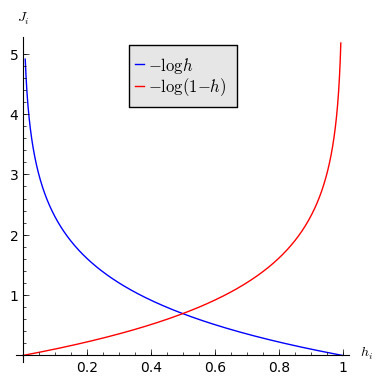
\[c(H(x), y) = \begin{cases} -\log(H(x)) & \text{if } y = 1 \\ -\log(1 - H(x)) & \text{if } y = 0 \end{cases}\]로 나눌 수 있다
따라서 H(X)는 X가 1인 확률을 나타낸다 볼 수 있다
\[H(X) \approx P(X = 1) ⇒ \frac{1}{1 + e^{-X \cdot W}}\]- H(X)=0.7이라면 70%의 확률로 1, H(X)=0.3이면 30%의 확률로 1
y가 1일 때의 함수의 그래프를 그려보게 되면 예측 값이 1에 가까워질수록 Cost Function의 값은 0에 가까워진다.
반대로 예측을 잘 못하여 0에 가까워질수록 Cost Function의 값이 무한대로 증가하게 되어 예측이 틀렸다는 것을 보여준다.
경사 하강법을 사용하여, 가장 적절한 예측을 하도록 W(가중치)를 최소화 하는 방향으로 업데이트 시킴
\[W := W - \alpha \frac{\partial}{\partial W} cost(W) = W - \alpha \nabla_W cost(W)\]Computing Hypothesis
Imports
1
2
3
4
5
6
7
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
# For reproducibility
torch.manual_seed(1)
Training Data
1
2
3
4
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]] # m = 6, d = 2
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
Computing the Hypothesis
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
print('e^1 equals: ', torch.exp(torch.FloatTensor([1]))) # 2.7183
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
hypothesis = 1 / (1 + torch.exp(-(x_train.matmul(W) + b)))
# x_train.matmul(W) == x*w == torch.matmal(x,w)
print(hypothesis)
print(hypothesis.shape)
# tensor([[0.5000],
# [0.5000],
# [0.5000],
# [0.5000],
# [0.5000],
# [0.5000]], grad_fn=<MulBackward>)
# torch.Size([6, 1])
기본값 0.5 가 나온다
시그모이드 함수는 pytorch에서 제공해준다
1
print('1/(1+e^{-1}) equals: ', torch.sigmoid(torch.FloatTensor([1]))) # 2.7183
Computing Cost Function
한 개의 element에 대해 계산하면 아래와 같이 나타남
1
2
-(y_train[0] * torch.log(hypothesis[0]) + (1 - y_train[0]) * torch.log(1 - hypothesis[0]))
# tensor([0.6931], grad_fn=<NegBackward>)
전체 샘플에 대해서 계산을 하면
1
2
3
4
5
6
7
8
9
10
11
12
13
losses = -(y_train * torch.log(hypothesis) +
(1 - y_train) * torch.log(1 - hypothesis))
print(losses)
# tensor([[0.6931],
# [0.6931],
# [0.6931],
# [0.6931],
# [0.6931],
# [0.6931]], grad_fn=<NegBackward>)
cost = losses.mean()
print(cost)
# tensor(0.6931, grad_fn=<MeanBackward1>)
pytorch에서 제공되는 함수를 사용하면 간단히 구현 가능
1
2
F.binary_cross_entropy(hypothesis, y_train)
# tensor(0.6931, grad_fn=<BinaryCrossEntropyBackward>)
Whole Training Procedure
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 모델 초기화
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# Cost 계산
hypothesis = torch.sigmoid(x_train.matmul(W) + b) # or .mm or @
cost = F.binary_cross_entropy(hypothesis, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
Evaluation
Loading Real Data
실제 데이터로 연습해보자
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
xy = np.loadtxt('data-03-diabetes.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
print(x_train[0:5])
print(y_train[0:5])
# tensor([[-0.2941, 0.4874, 0.1803, -0.2929, 0.0000, 0.0015, -0.5312, -0.0333],
# [-0.8824, -0.1457, 0.0820, -0.4141, 0.0000, -0.2072, -0.7669, -0.6667],
# [-0.0588, 0.8392, 0.0492, 0.0000, 0.0000, -0.3055, -0.4927, -0.6333],
# [-0.8824, -0.1055, 0.0820, -0.5354, -0.7778, -0.1624, -0.9240, 0.0000],
# [ 0.0000, 0.3769, -0.3443, -0.2929, -0.6028, 0.2846, 0.8873, -0.6000]])
# tensor([[0.],
# [1.],
# [0.],
# [1.],
# [0.]])
학습 과정
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 모델 초기화
W = torch.zeros((8, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=1)
nb_epochs = 100
for epoch in range(nb_epochs + 1):
# Cost 계산
# hypothesis = torch.sigmoid(x_train.matmul(W) + b) # or .mm or @
# cost = -(y_train * torch.log(hypothesis) + (1 - y_train) * torch.log(1 - hypothesis)).mean()
hypothesis = torch.sigmoid(x_train.matmul(W) + b) # or .mm or @
cost = F.binary_cross_entropy(hypothesis, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 10번마다 로그 출력
if epoch % 10 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
학습 평가
1
2
3
4
5
6
7
hypothesis = torch.sigmoid(x_test.matmul(W) + b)
print(hypothesis[:5])
# tensor([[0.4103],
# [0.9242],
# [0.2300],
# [0.9411],
# [0.1772]], grad_fn=<SliceBackward>)
확률을 바이너리 값으로 예측
1
2
3
4
5
6
7
prediction = hypothesis >= torch.FloatTensor([0.5])
print(prediction[:5])
# tensor([[0],
# [1],
# [0],
# [1],
# [0]], dtype=torch.uint8)
결과 비교
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
print(prediction[:5])
print(y_train[:5])
# tensor([[0],
# [1],
# [0],
# [1],
# [0]], dtype=torch.uint8)
# tensor([[0.],
# [1.],
# [0.],
# [1.],
# [0.]])
correct_prediction = prediction.float() == y_train
print(correct_prediction[:5])
# tensor([[1],
# [1],
# [1],
# [1],
# [1]], dtype=torch.uint8)
적중률 표현
1
2
3
accuracy = correct_prediction.sum().item() / len(correct_prediction)
print('The model has an accuracy of {:2.2f}% for the training set.'.format(accuracy * 100))
# The model has an accuracy of 76.68% for the training set.
Higher Implementation
실전에서는 class를 이용해서 구현함
1
2
3
4
5
6
7
8
9
class BinaryClassifier(nn.Module): # nn.Module 상
def __init__(self):
super().__init__()
self.linear = nn.Linear(8, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
return self.sigmoid(self.linear(x))
model = BinaryClassifier()
선언한 model을 이용한 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import numpy as np
# For reproducibility
torch.manual_seed(1)
class BinaryClassifier(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(8, 1) # self.linear = {W, b} , m = ?, d = 8
self.sigmoid = nn.Sigmoid()
def forward(self, x):
return self.sigmoid(self.linear(x))
model = BinaryClassifier()
xy = np.loadtxt('data-03-diabetes.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
W = torch.zeros((8, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
# optimizer = optim.SGD([W, b], lr=1)
optimizer = optim.SGD(model.parameters(), lr=1)
nb_epochs = 100
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = model(x_train)
# cost 계산
cost = F.binary_cross_entropy(hypothesis, y_train)
# Cost 계산
# hypothesis = torch.sigmoid(x_train.matmul(W) + b) # or .mm or @
# cost = F.binary_cross_entropy(hypothesis, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
if epoch % 10 == 0:
prediction = hypothesis >= torch.FloatTensor([0.5])
correct_prediction = prediction.float() == y_train
accuracy = correct_prediction.sum().item() / len(correct_prediction)
print('Epoch {:4d}/{} Cost: {:.6f} Accuracy {:2.2f}%'.format(
epoch, nb_epochs, cost.item(), accuracy * 100,
))
# Epoch 0/100 Cost: 0.704829 Accuracy 45.72%
# Epoch 10/100 Cost: 0.572391 Accuracy 67.59%
# Epoch 20/100 Cost: 0.539563 Accuracy 73.25%
# Epoch 30/100 Cost: 0.520042 Accuracy 75.89%
# Epoch 40/100 Cost: 0.507561 Accuracy 76.15%
# Epoch 50/100 Cost: 0.499125 Accuracy 76.42%
# Epoch 60/100 Cost: 0.493177 Accuracy 77.21%
# Epoch 70/100 Cost: 0.488846 Accuracy 76.81%
# Epoch 80/100 Cost: 0.485612 Accuracy 76.28%
# Epoch 90/100 Cost: 0.483146 Accuracy 76.55%
# Epoch 100/100 Cost: 0.481234 Accuracy 76.81%
This post is licensed under CC BY 4.0 by the author.