[모두를 위한 딥러닝 시즌2] Lab-06 Softmax Classification

Posted Oct 16, 2024

By 띵석

views 11 min read

Softmax

Import

  
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# For reproducibility
torch.manual_seed(1)

Discrete Probability Distribution

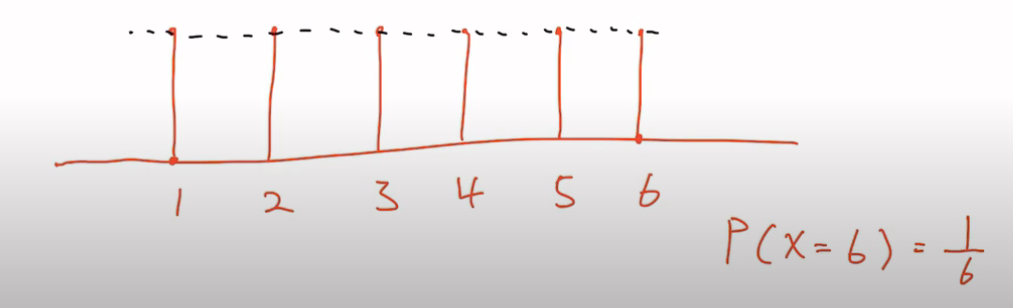
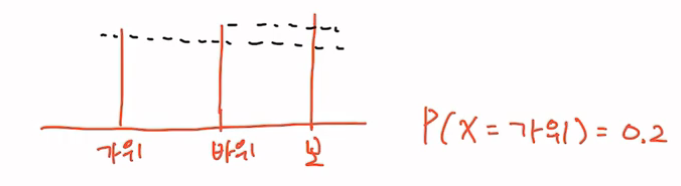
이산적인 확률 분포
- 주사위, 가위바위보, 동전 던지기

Softmax

이산적인 확률 분포를 바탕으로 다음 행동을 예측 (패턴)하는 머신러닝을 수행함
- 확률 분포를 신경망(Neural Network, NN) 또는 선형 모델(Linear Model)을 이용해 근사
- Max값을 Soft하게 뽑아줌

\[P(class = i) = \frac{e^i} {∑e^i}\]

  
# softmax 미적용
z = torch.FloatTensor([1, 2, 3])
# max = (0, 0, 1)

hypothesis = F.softmax(z, dim=0)
print(hypothesis)
# tensor([0.0900, 0.2447, 0.6652])
0.09 = \frac {e^1}{e^1 + e^2 + e^3}

hypothesis.sum() # softmax 값의 합
# tensor(1.) # 1이 나온다

$0.09 = \frac {e^1}{e^1 + e^2 + e^3}$의 값을 확인 가능

Cross Entropy

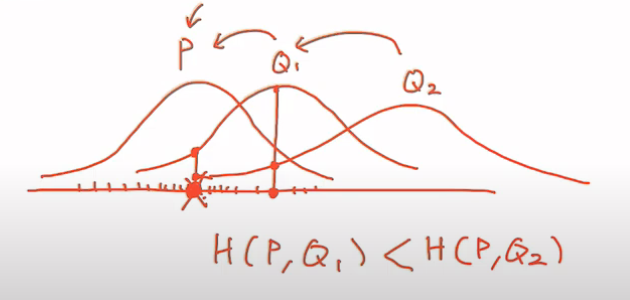
\[H(P, Q) = -\mathbb{E}{x \sim P(x)}[\log Q(x)] = -\sum{x \in \mathcal{X}} P(x) \log Q(x)\]

확률분포 P에서 x를 샘플링
샘플링한 x를 Q에 넣음
log를 씌운 값의 평균을 구함

Q2 → Q1, Q1 → P 로 갈 수 있도록 (근사) 크로스 엔트로피를 최소화시키는것이 중요

Low-level Implementation

Cross Entropy Loss (Low-level)

크로스 엔트로피의 Loss 수식

$y = P(x)$ (실제 값)
$\hat{y} = Q(x) = \mathbb{P}{\theta}(x)$

\[L = \frac{1}{N} \sum -y \log(\hat{y})\]

  
z = torch.rand(3, 5, requires_grad=True) # 3, 5 rand 
hypothesis = F.softmax(z, dim=1) # 두번째 dim(행)에 대해 softmax
print(hypothesis)
# tensor([[0.2645, 0.1639, 0.1855, 0.2585, 0.1277],
#         [0.2430, 0.1624, 0.2322, 0.1930, 0.1694],
#         [0.2226, 0.1986, 0.2326, 0.1594, 0.1868]], grad_fn=<SoftmaxBackward>)

y = torch.randint(5, (3,)).long() # 임의로 만든 정답
print(y)
# tensor([0, 2, 1]) == 0.2645, 0.1986, 0.2322

y_one_hot = torch.zeros_like(hypothesis) # |y_one_hot| = (3, 5)
y_one_hot.scatter_(1, y.unsqueeze(1), 1) # |y| = (3,) , y.unsqueeze(1) = (3,1)
print(cost)
# tensor([[1., 0., 0., 0., 0.],
#         [0., 0., 1., 0., 0.],
#         [0., 1., 0., 0., 0.]])

cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
print(cost)
# tensor(1.4689, grad_fn=<MeanBackward1>)

Cross Entropy Loss with torch.nn.runctional

pytorch는 softmax, log_softmax를 제공

  
# Low level
torch.log(F.softmax(z, dim=1))
# tensor([[-1.3301, -1.8084, -1.6846, -1.3530, -2.0584],
#         [-1.4147, -1.8174, -1.4602, -1.6450, -1.7758],
#         [-1.5025, -1.6165, -1.4586, -1.8360, -1.6776]], grad_fn=<LogBackward>)
# High level
F.log_softmax(z, y)
# tensor([[-1.3301, -1.8084, -1.6846, -1.3530, -2.0584],
#         [-1.4147, -1.8174, -1.4602, -1.6450, -1.7758],
#         [-1.5025, -1.6165, -1.4586, -1.8360, -1.6776]], grad_fn=<LogBackward>)

(y_one_hot * -torch.log(F.softmax(z, dim=1))).sum(dim=1).mean()
# tensor(1.4689, grad_fn=<MeanBackward1>)

F.nll_loss(F.log_softmax(z, dim=1), y) # Negative Log Likelihood
# tensor(1.4689, grad_fn=<NllLossBackward>)

F.cross_entropy(z, y)
# tensor(1.4689, grad_fn=<NllLossBackward>)

Training with Low-level Cross Entropy Loss

최적화

  
# |x_train| = (m, 차원 d = 4)
# |y_train| = (m,)
x_train = [[1, 2, 1, 1],
           [2, 1, 3, 2],
           [3, 1, 3, 4],
           [4, 1, 5, 5],
           [1, 7, 5, 5],
           [1, 2, 5, 6],
           [1, 6, 6, 6],
           [1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0] # one_hot 벡터로 나타내었을 때 1이 있는 위치의 index  값
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train) # 우리는 이산 확률 분포를 근사하고있기 때문에 정수형인 LongTensor로 바꿔 준다

# 모델 초기화
W = torch.zeros((4, 3), requires_grad=True) # samples = 4, classes = 3, dim = 4
b = torch.zeros(1, requires_grad=True)

# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    hypothesis = F.softmax(x_train.matmul(W) + b, dim=1) # logistic regression
    y_one_hot = torch.zeros_like(hypothesis)
    y_one_hot.scatter_(1, y_train.unsqueeze(1), 1)
    cost = (y_one_hot * -torch.log(F.softmax(hypothesis, dim=1))).sum(dim=1).mean() # loss

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward() #backpropagation
    optimizer.step() # w, b에 대해 lr = 0.1 one step Stochastic Gradient Descent

    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))
        
        # Epoch    0/1000 Cost: 1.098612
				# Epoch  100/1000 Cost: 0.901535
				# Epoch  200/1000 Cost: 0.839114
				# Epoch  300/1000 Cost: 0.807826
				# Epoch  400/1000 Cost: 0.788472
				# Epoch  500/1000 Cost: 0.774822
				# Epoch  600/1000 Cost: 0.764449
				# Epoch  700/1000 Cost: 0.756191
				# Epoch  800/1000 Cost: 0.749398
				# Epoch  900/1000 Cost: 0.743671
				# Epoch 1000/1000 Cost: 0.738749

High-level Implementation

Training with `F.cross_entropy`

좀더 쉽게 구현하기

  
# 모델 초기화
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    z = x_train.matmul(W) + b # or .mm or @
    cost = F.cross_entropy(z, y_train) # F.cross_entropy를 통해 바로 정답과 비교
    # one hot 벡터를 만들어주는 과정이 생략되어 scatter는 필요없음

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))
        # Epoch    0/1000 Cost: 1.098612
				# Epoch  100/1000 Cost: 0.761050
				# Epoch  200/1000 Cost: 0.689991
				# Epoch  300/1000 Cost: 0.643229
				# Epoch  400/1000 Cost: 0.604117
				# Epoch  500/1000 Cost: 0.568255
				# Epoch  600/1000 Cost: 0.533922
				# Epoch  700/1000 Cost: 0.500291
				# Epoch  800/1000 Cost: 0.466908
				# Epoch  900/1000 Cost: 0.433507
				# Epoch 1000/1000 Cost: 0.399962

High-level Implementation with `nn.Module`

실전에 가깝게 더 쉽게 구현하기

  
class SoftmaxClassifierModel(nn.Module):
    def __init__(self):
        super().__init__()
        # 4 -> 3
        # 4개의 input을 받아서 3개의 class에 대한 각각의 확률값
        self.linear = nn.Linear(4, 3) # Output이 3!
        
        
    def forward(self, x):
        return self.linear(x) # |X| = (m, 4) => (m, 3)
        
model = SoftmaxClassifierModel()
 
 # optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    # H(x) 계산
    prediction = model(x_train) #|X-train| = (m, 4), |prediction| = (m, 4)
    

    # cost 계산
    cost = F.cross_entropy(prediction, y_train) # |y_train| = (m, )

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
    # 20번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))
        # Epoch    0/1000 Cost: 1.849513
				# Epoch  100/1000 Cost: 0.689894
				# Epoch  200/1000 Cost: 0.609259
				# Epoch  300/1000 Cost: 0.551218
				# Epoch  400/1000 Cost: 0.500141
				# Epoch  500/1000 Cost: 0.451947
				# Epoch  600/1000 Cost: 0.405051
				# Epoch  700/1000 Cost: 0.358733
				# Epoch  800/1000 Cost: 0.312912
				# Epoch  900/1000 Cost: 0.269521
				# Epoch 1000/1000 Cost: 0.241922

Softmax Classification 은 Logistic Regression과 굉장히 유사

Logistic Regression
- Binary Classification 에서 사용
- 두 가지 클래스(0과 1)만 존재하는 경우
- 예측된 확률이 0.5 이상이면 해당 클래스로 분류
- Binary Cross-Entropy 와 Sigmoid 함수 사용
Softmax Classification
- Multi-class Classification 에서 사용
- 여러 개의 클래스가 존재할 때
- 출력 값은 각 클래스에 속할 확률
- Cross-Entropy 와 Softmax 함수 사용

Training Example

실습하기

Data

  
xy **=** np**.**loadtxt('data-04-zoo.csv', delimiter**=**',', dtype**=**np**.**float32)

x_train = torch.FloatTensor(xy[:, 0:-1])
y_train = torch.LongTensor(xy[:, [-1]]).squeeze()

print(x_train.shape) # x_train shape
print(len(x_train))  # x_train 길이
print(x_train[:5])   # 첫 다섯 개
# torch.Size([101, 16])
# 101
# tensor([[1., 0., 0., 1., 0., 0., 1., 1., 1., 1., 0., 0., 4., 0., 0., 1.],
#         [1., 0., 0., 1., 0., 0., 0., 1., 1., 1., 0., 0., 4., 1., 0., 1.],
#         [0., 0., 1., 0., 0., 1., 1., 1., 1., 0., 0., 1., 0., 1., 0., 0.],
#         [1., 0., 0., 1., 0., 0., 1., 1., 1., 1., 0., 0., 4., 0., 0., 1.],
#         [1., 0., 0., 1., 0., 0., 1., 1., 1., 1., 0., 0., 4., 1., 0., 1.]])

torch.Size([101])
101
tensor([0, 0, 3, 0, 0])
# nb_classes = 7
# y_one_hot = torch.zeros((len(y_train), nb_classes))
# y_one_hot = y_one_hot.scatter(1, y_train.unsqueeze(1), 1)

Training with `F.cross_entropy`

  
# 모델 초기화
W = torch.zeros((16, 7), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    # Cost 계산 (2)
    z = x_train.matmul(W) + b # or .mm or @
    cost = F.cross_entropy(z, y_train)

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

High-level Implementation with `nn.Module`

  
class SoftmaxClassifierModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(16, 7)
    def forward(self, x):
        return self.linear(x)
        
model = SoftmaxClassifierModel()

# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    # H(x) 계산
    prediction = model(x_train)

    # cost 계산
    cost = F.cross_entropy(prediction, y_train)

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
    # 20번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

전체 코드

  
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# 모델 class
class SoftmaxClassifierModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(16, 7)
    def forward(self, x):
        return self.linear(x)
       
# 데이터
xy = np.loadtxt('data-04-zoo.csv', delimiter=',', dtype=np.float32)
x_train = torch.FloatTensor(xy[:, 0:-1])
y_train = torch.LongTensor(xy[:, [-1]]).squeeze()

# 모델 초기화
model = SoftmaxClassifierModel()

# For reproducibility
torch.manual_seed(1)

# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    # H(x) 계산
    prediction = model(x_train)

    # cost 계산
    cost = F.cross_entropy(prediction, y_train)

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
    # 20번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))
        # Epoch    0/1000 Cost: 2.167349
        # Epoch  100/1000 Cost: 0.478046
        # Epoch  200/1000 Cost: 0.322867
        # Epoch  300/1000 Cost: 0.249685
        # Epoch  400/1000 Cost: 0.204888
        # Epoch  500/1000 Cost: 0.174191
        # Epoch  600/1000 Cost: 0.151702
        # Epoch  700/1000 Cost: 0.134461
        # Epoch  800/1000 Cost: 0.120799
        # Epoch  900/1000 Cost: 0.109696
        # Epoch 1000/1000 Cost: 0.100488

Study, AI

This post is licensed under CC BY 4.0 by the author.

Softmax

Import

Discrete Probability Distribution

Softmax

Cross Entropy

Low-level Implementation

Cross Entropy Loss (Low-level)

Cross Entropy Loss with torch.nn.runctional

Training with Low-level Cross Entropy Loss

High-level Implementation

Training with F.cross_entropy

High-level Implementation with nn.Module

Training Example

Data

Training with F.cross_entropy

High-level Implementation with nn.Module

Trending Tags

Training with `F.cross_entropy`

High-level Implementation with `nn.Module`

Training with `F.cross_entropy`

High-level Implementation with `nn.Module`