Post

[모두를 위한 딥러닝 시즌2] Lab-08-2 Multi Layer Perceptron

Posted
By 띵석
views 9 min read
[모두를 위한 딥러닝 시즌2] Lab-08-2 Multi Layer Perceptron

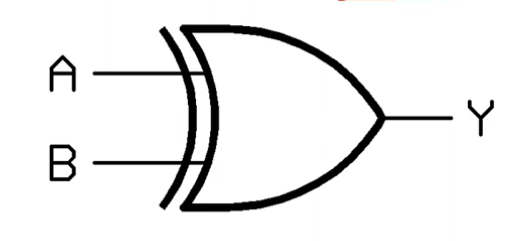
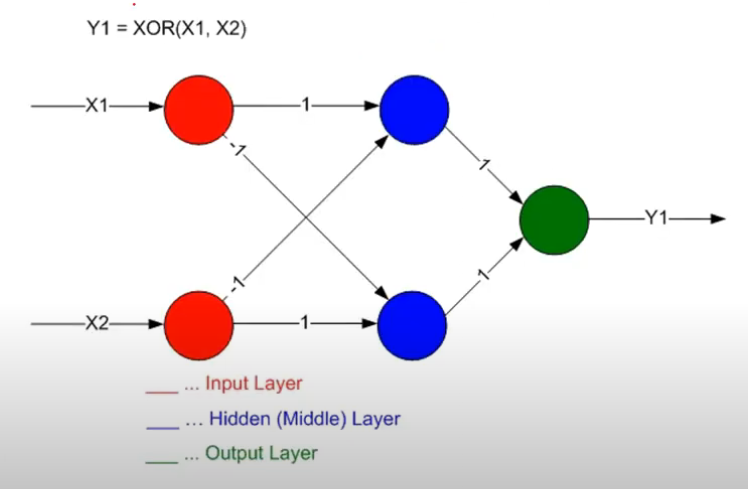
Review : XOR

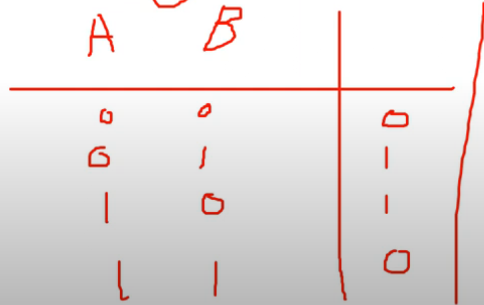
image.png

image.png

  • XOR : 입력이 같으면 0, 다르면 1을 출력
  • 단층 퍼셉트론(선형)으로는 XOR 문제를 해결할 수 없음 (Marvin Minsky, Perceptrons)

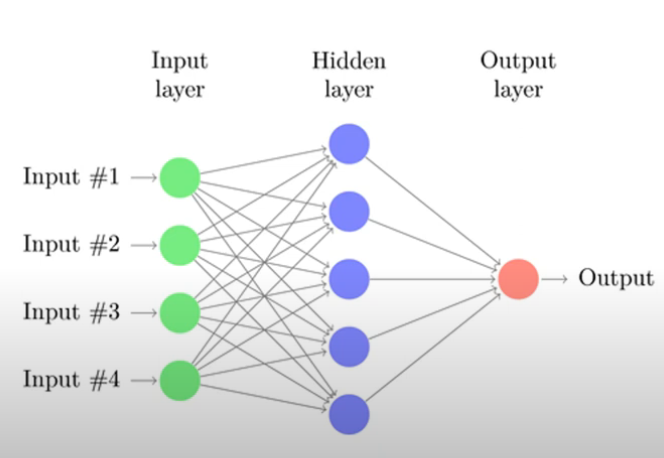
Multi Layer Perceptron

  • 여러 개의 층(layer)을 가지는 구조
  • 단층 퍼셉트론으로는 해결할 수 없는 비선형 문제를 해결할 수 있음

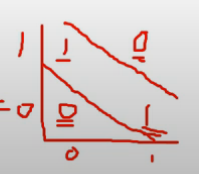
image.png

  • 선(결정 경계)을 더 추가함으로써 XOR 문제를 해결할 수 있음

image.png

하지만, 당시에는 MLP를 학습할 방법이 없었기 때문에 인공지능 연구는 한동안 발전하지 못함(인공지능의 암흑기)

문제점

  1. 순전파로는 출력값만 계산할 수 있고, 출력값이 정답과 얼마나 차이가 나는지(즉, 오차)를 통해 가중치를 어떻게 업데이트해야 하는지 알 수 없음.
  2. 오차 정보를 가중치에 반영하는 방법이 없음. 각 가중치가 출력값에 어떻게 기여하는지(즉, 가중치가 출력에 미치는 영향)를 계산할 수 없음
  3. 기울기(Gradient)를 계산할 수 없음. 신경망을 학습하려면 손실 함수의 기울기(미분 값)를 계산하고, 이를 바탕으로 가중치를 업데이트해야 하는데, 순전파만으로는 각 가중치가 출력에 미치는 영향을 계산할 수 없기 때문에 기울기를 계산할 수 없음

Backpropagation

  • 오차(Loss)를 계산한 후, 이를 바탕으로 신경망의 가중치를 업데이트하는 방법
  • 연쇄 법칙(Chain Rule)을 사용해 각 가중치에 대한 기울기를 계산
  • 경사 하강법(Gradient Descent)으로 가중치를 갱신

과정

  1. 입력 데이터 $X$를 신경망에 넣어 예측 값 $Y_{\text{pred}}$을 구함 (순전파)
  2. 예측 값과 실제 값 $Y_{\text{true}}$ 간의 오차를 계산
  3. 오차에 대해 각 가중치에 대한 미분 값(기울기) $\frac{\partial \text{Loss}}{\partial W}$를 계산하여, 경사 하강법으로 가중치를 업데이트

image.png

코드 구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

import torch
device = 'cuda' if torch.cuda.is_available() else 'cpu'

# for reproducibility
torch.manual_seed(777)
if device == 'cuda':
    torch.cuda.manual_seed_all(777)

# XOR 
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)

# nn layers
linear1 = torch.nn.Linear(2, 2, bias=True)
linear2 = torch.nn.Linear(2, 1, bias=True) #추가됨
sigmoid = torch.nn.Sigmoid()

# model
model = torch.nn.Sequential(linear1, sigmoid, linear2, sigmoid).to(device)

# define cost/loss & optimizer
criterion = torch.nn.BCELoss().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=1)  # modified learning rate from 0.1 to 1

#학습
for step in range(10001):
    optimizer.zero_grad()
    hypothesis = model(X)

    # cost/loss function
    cost = criterion(hypothesis, Y)
    cost.backward()
    optimizer.step()

    if step % 100 == 0:
        print(step, cost.item())
# 0 0.7434073090553284
# 100 0.693165123462677
# 200 0.6931577920913696
# 300 0.6931517124176025
# ...
# 9800 0.0012681199004873633
# 9900 0.0012511102249845862
# 10000 0.0012345188297331333
        
        
# Accuracy computation
# True if hypothesis>0.5 else False
with torch.no_grad():
    hypothesis = model(X)
    predicted = (hypothesis > 0.5).float()
    accuracy = (predicted == Y).float().mean()
    print('\nHypothesis: ', hypothesis.detach().cpu().numpy(), '\nCorrect: ', predicted.detach().cpu().numpy(), '\nAccuracy: ', accuracy.item())

# Hypothesis:  [[0.00106364]
#  [0.99889404]
#  [0.99889404]
#  [0.00165861]] 
# Correct:  [[0.]
#  [1.]
#  [1.]
#  [0.]] 
# Accuracy:  1.0

Code : xor-nn

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

import torch
device = 'cuda' if torch.cuda.is_available() else 'cpu'

# for reproducibility
torch.manual_seed(777)
if device == 'cuda':
    torch.cuda.manual_seed_all(777)

# XOR 
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)

# nn layers
linear1 = torch.nn.Linear(2, 2, bias=True)
linear2 = torch.nn.Linear(2, 1, bias=True) #추가됨
sigmoid = torch.nn.Sigmoid()

# model
model = torch.nn.Sequential(linear1, sigmoid, linear2, sigmoid).to(device)

# define cost/loss & optimizer
criterion = torch.nn.BCELoss().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=1)  # modified learning rate from 0.1 to 1

#학습
for step in range(10001):
    optimizer.zero_grad()
    hypothesis = model(X)

    # cost/loss function
    cost = criterion(hypothesis, Y)
    cost.backward()
    optimizer.step()

    if step % 100 == 0:
        print(step, cost.item())
# 0 0.7434073090553284
# 100 0.693165123462677
# 200 0.6931577920913696
# 300 0.6931517124176025
# ...
# 9800 0.0012681199004873633
# 9900 0.0012511102249845862
# 10000 0.0012345188297331333
        
        
# Accuracy computation
# True if hypothesis>0.5 else False
with torch.no_grad():
    hypothesis = model(X)
    predicted = (hypothesis > 0.5).float()
    accuracy = (predicted == Y).float().mean()
    print('\nHypothesis: ', hypothesis.detach().cpu().numpy(), '\nCorrect: ', predicted.detach().cpu().numpy(), '\nAccuracy: ', accuracy.item())

# Hypothesis:  [[0.00106364]
#  [0.99889404]
#  [0.99889404]
#  [0.00165861]] 
# Correct:  [[0.]
#  [1.]
#  [1.]
#  [0.]] 
# Accuracy:  1.0

Code : xor-nn-wide-deep

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

import torch
device = 'cuda' if torch.cuda.is_available() else 'cpu'

# for reproducibility
torch.manual_seed(777)
if device == 'cuda':
    torch.cuda.manual_seed_all(777)

# XOR 
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)

# nn layers
linear1 = torch.nn.Linear(2, 10, bias=True)
linear2 = torch.nn.Linear(10, 10, bias=True)
linear3 = torch.nn.Linear(10, 10, bias=True)
linear4 = torch.nn.Linear(10, 1, bias=True) # 레이어가 4개
sigmoid = torch.nn.Sigmoid()

# model
model = torch.nn.Sequential(linear1, sigmoid, linear2, sigmoid, linear3, sigmoid, linear4, sigmoid).to(device)

# define cost/loss & optimizer
criterion = torch.nn.BCELoss().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=1)  # modified learning rate from 0.1 to 1

#학습
for step in range(10001):
    optimizer.zero_grad()
    hypothesis = model(X)

    # cost/loss function
    cost = criterion(hypothesis, Y)
    cost.backward()
    optimizer.step()

    if step % 100 == 0:
        print(step, cost.item())
# 0 0.6948983669281006
# 100 0.693155825138092
# 200 0.6931535601615906
# 300 0.6931513547897339
# ...
# 9800 0.00016420979227405041
# 9900 0.00016027523088268936
# 10000 0.00015648972475901246
# 레이어가 2개일 때보다 더 작은 loss 확인
        
# Accuracy computation
# True if hypothesis>0.5 else False
with torch.no_grad():
    hypothesis = model(X)
    predicted = (hypothesis > 0.5).float()
    accuracy = (predicted == Y).float().mean()
    print('\nHypothesis: ', hypothesis.detach().cpu().numpy(), '\nCorrect: ', predicted.detach().cpu().numpy(), '\nAccuracy: ', accuracy.item())

# Hypothesis:  [[1.1168801e-04]
#  [9.9982882e-01]
#  [9.9984229e-01]
#  [1.8529482e-04]] 
# Correct:  [[0.]
#  [1.]
#  [1.]
#  [0.]] 
# Accuracy:  1.0

MLP에서 레이어와 뉴런 개수 정하기

Layer의 개수:

  • 간단한 문제는 1~2개의 레이어로 충분 (예: XOR 문제)
  • 복잡한 문제는 더 많은 레이어가 필요할 수 있음 (예: 이미지 인식, 자연어 처리)
  • 실험적 접근 : 교차 검증을 통해 여러 가지 레이어 구성을 실험하여 최적의 성능을 찾음

Layer의 뉴런 수:

  • 첫 번째 레이어의 뉴런 수는 입력 데이터의 차원과 관련
    • 예: 입력 데이터가 100차원이라면 첫 번째 레이어는 최소 100개의 뉴런이 필요할 수 있음
  • 마지막 레이어의 뉴런 수는 출력 데이터의 차원과 일치
    • 예: 이진 분류 문제라면 마지막 레이어에는 1개의 뉴런이 필요하고, 다중 클래스 분류 문제라면 출력 클래스의 개수만큼 뉴런이 필요
  • 중간 레이어는 점진적으로 뉴런 수를 줄여가는 방식이 일반적이며, 실험적으로 결정됨

결정 시 고려 요소:

  • 과적합: 레이어나 뉴런 수가 너무 많으면 모델이 과적합될 수 있으므로, 정규화(regularization)와 드롭아웃(dropout)을 사용해 방지
  • 컴퓨팅 자원: 레이어나 뉴런 수가 많아지면 계산 자원이 더 필요하므로, 메모리와 연산 시간을 고려해야 함
  • 문제의 특성: 문제의 복잡도에 따라 레이어의 개수와 뉴런 수가 달라짐. 복잡한 비선형 패턴을 학습할 경우 더 많은 레이어와 뉴런이 필요할 수 있음
Study, AI
Deep Learning Zero To All 모두를 위한 딥러닝 시즌2 ML DL pytorch
This post is licensed under CC BY 4.0 by the author.