[모두를 위한 딥러닝 시즌2] Lab-09-2 Weight initialization
[모두를 위한 딥러닝 시즌2] Lab-09-2 Weight initialization
Why good initialization?
- 제프리 힌튼 : We initialized the weights in a stupid way
- 기존의 무작위 가중치 초기화는 비효율적인 방식이었음
- 체계적인 가중치 초기화가 모델의 성능 향상에 큰 영향을 미침
- 모든 가중치를 0으로 초기화할 경우 역전파 과정에서 모든 그래디언트가 0이 되어 학습이 불가능해진다
- 초기 가중치가 너무 크거나 작으면 기울기가 너무 커지거나 작아져서 기울기 폭주나 소실 문제가 발생
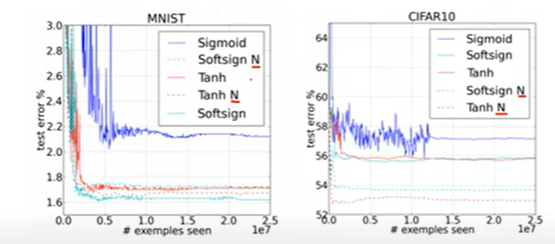
DataSet 학습 비교
N = Weight initialization 적용한 방식
가중치 초기화 방법을 적용한 모델이 성능이 뛰어남
RBM (Restricted Boltzmann Machine) / DBN (Deep Belief Network)
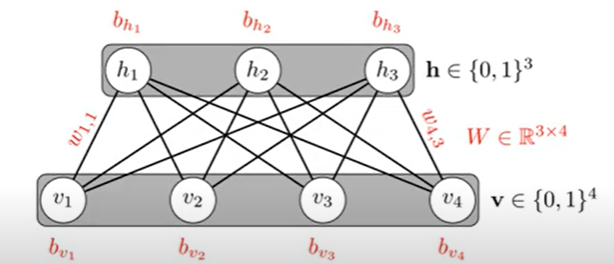
RBN
- 같은 레이어 내에서는 연결이 없다
- 레이어 간에는 완전 연결
- 순방향(encoding)과 역방향(decoding) 과정을 통한 학습
- 입력 데이터 x로부터 은닉층 표현 y를 생성
- y로부터 x를 복원한 x’ 생성
DBN
여러 층의 제한 볼츠만 머신(RBM)을 쌓아서 구성된 딥러닝 모델
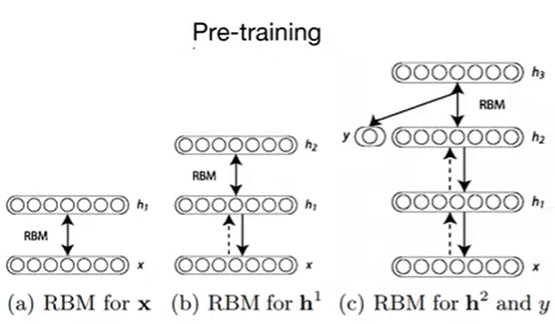
- 사전 학습 (Pre-training)
- 입력 x와 첫 번째 은닉층 h1을 RBM으로 학습
- 학습이 완료되면, x와 h1 간의 가중치는 고정시킨다
- h1과 h2를 RBM으로 학습
- 이 과정을 여러 층에 걸쳐 반복
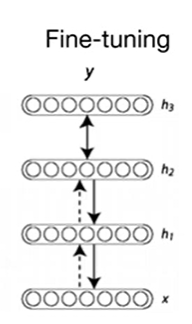
- 파인튜닝 (Fine-Tuning)
- 사전 학습이 완료된 후, 일반적인 역전파 알고리즘을 사용하여 네트워크를 학습
- 전체 네트워크 미세조정
의의
- RBM을 사용한 사전 학습은 현재 많이 사용되지 않음
- 하지만 깊은 신경망의 학습을 가능하게 했고, 이는 현대 딥러닝의 발전에 중요한 이정표 역할을 함
Xavier(Glorot) / He initialization
- RBM 기반의 사전 학습은 복잡하다
- 이를 단순화하기 위해 Xavier(2015)와 He(2010) 초기화와 같은 기법이 등장
균등 분포 (Uniform Distribution)
- 지정된 범위 내에서 모든 값이 발생할 확률이 동일한 분포
- 장점
- 대칭성 깨기: 뉴런들이 서로 다른 특징을 학습하도록 함
- 탐색 효율성: 다양한 가중치 값으로 인해 파라미터 공간에서 효율적 탐색이 가능
- 단점
- 초기화 범위에 매우 민감
- 범위가 너무 크면 그래디언트 폭주
- 범위가 너무 작으면 그래디언트 소실
- 적용:
torch.nn.init.uniform_(tensor, a=0.0, b=1.0)
정규 분포 (Normal Distribution)
- 평균이 0이고 지정된 표준편차를 가지는 정규분포로 초기화
- 장점
- 가중치 다양성: 가중치에 다양성을 부여하여 네트워크가 다양한 패턴을 학습
- 그래디언트 전파: 적절한 표준편차 선택을 통해 그래디언트 소실 및 폭주 문제를 줄일 수 있음
- 단점
- 민감한 하이퍼파라미터: 표준편차 선택이 신경망 성능에 크게 영향을 미칠 수 있음
- 적절한 값 설정의 어려움: 실험을 통해 최적의 값을 찾아야
- 적용:
torch.nn.init.normal_(tensor, mean=0.0, std=1.0)
Xavier 초기화
- 입력과 출력 노드 수를 모두 고려
- 선형 활성화 함수(sigmoid, tanh)에 최적화
- 각 층의 출력이 적절한 분산을 유지하도록 설계
정규 분포를 기반으로 가중치 초기화
$W \sim N(0, \text{Var}(W)) \quad, \quad \text{Var}(W) = \sqrt\frac{2}{n_{in} + n_{out}}$
균등 분포를 기반으로 가중치 초기화
$W \sim U\left(-\frac{\sqrt{6}}{\sqrt{n_{in} + n_{out}}}, +\frac{\sqrt{6}}{\sqrt{n_{in} + n_{out}}}\right)$
He 초기화
- 입력 노드 수만 고려
- ReLU 계열 활성화 함수에 최적화
- 더 큰 초기 가중치 값 허용
정규 분포를 기반으로 가중치 초기화
$W \sim N(0, \text{Var}(W)) \quad, \quad \text{Var}(W) = \sqrt\frac{2}{n_{in}}$
균등 분포를 기반으로 가중치 초기화
$W \sim U\left(-\frac{\sqrt{6}}{\sqrt{n_{in}}}, +\frac{\sqrt{6}}{\sqrt{n_{in}}}\right)$
차이점
| Xavier Initialization | He Initialization | |
|---|---|---|
| 활성화 함수 | 시그모이드(Sigmoid), 하이퍼볼릭 탄젠트(Tanh) | ReLU 및 변형 활성화 함수 (Leaky ReLU, PReLU 등) |
| 목적 | 네트워크에서 입력과 출력의 균형을 유지 | ReLU 활성화 함수에서 그래디언트 소실 문제 해결 |
| 적용 범위 | 얕은 네트워크 및 선형 활성화 함수에 적합 | 얕은 네트워크 및 선형 활성화 함수에 적합 |
| 분산 계산 | 입력과 출력 노드 수의 평균 사용 $(n_{in} + n_{out})$ | He: 입력 노드 수만 사용 $(n_{in})$ |
Code : mnist_nn_xavier
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
import torch
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import random
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# for reproducibility
random.seed(777)
torch.manual_seed(777)
if device == 'cuda':
torch.cuda.manual_seed_all(777)
# parameters
learning_rate = 0.001
training_epochs = 15
batch_size = 100
# MNIST dataset
mnist_train = dsets.MNIST(root='MNIST_data/',
train=True,
transform=transforms.ToTensor(),
download=True)
mnist_test = dsets.MNIST(root='MNIST_data/',
train=False,
transform=transforms.ToTensor(),
download=True)
# dataset loader
data_loader = torch.utils.data.DataLoader(dataset=mnist_train,
batch_size=batch_size,
shuffle=True,
drop_last=True)
# nn layers
linear1 = torch.nn.Linear(784, 256, bias=True)
linear2 = torch.nn.Linear(256, 256, bias=True)
linear3 = torch.nn.Linear(256, 10, bias=True)
relu = torch.nn.ReLU()
# xavier initialization
torch.nn.init.xavier_uniform_(linear1.weight)
torch.nn.init.xavier_uniform_(linear2.weight)
torch.nn.init.xavier_uniform_(linear3.weight)
# model
model = torch.nn.Sequential(linear1, relu, linear2, relu, linear3).to(device)
# define cost/loss & optimizer
criterion = torch.nn.CrossEntropyLoss().to(device) # Softmax is internally computed.
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
total_batch = len(data_loader)
for epoch in range(training_epochs):
avg_cost = 0
for X, Y in data_loader:
# reshape input image into [batch_size by 784]
# label is not one-hot encoded
X = X.view(-1, 28 * 28).to(device)
Y = Y.to(device)
optimizer.zero_grad()
hypothesis = model(X)
cost = criterion(hypothesis, Y)
cost.backward()
optimizer.step()
avg_cost += cost / total_batch
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.9f}'.format(avg_cost))
print('Learning finished')
# Epoch: 0001 cost = 0.246731028
# Epoch: 0002 cost = 0.092913948
# Epoch: 0003 cost = 0.060899034
# Epoch: 0004 cost = 0.044170324
# Epoch: 0005 cost = 0.032506533
# Epoch: 0006 cost = 0.025267148
# Epoch: 0007 cost = 0.020803869
# Epoch: 0008 cost = 0.018919067
# Epoch: 0009 cost = 0.014367993
# Epoch: 0010 cost = 0.014033089
# Epoch: 0011 cost = 0.014649723
# Epoch: 0012 cost = 0.013518972
# Epoch: 0013 cost = 0.009880106
# Epoch: 0014 cost = 0.007329788
# Epoch: 0015 cost = 0.011024385
# Test the model using test sets
with torch.no_grad():
X_test = mnist_test.test_data.view(-1, 28 * 28).float().to(device)
Y_test = mnist_test.test_labels.to(device)
prediction = model(X_test)
correct_prediction = torch.argmax(prediction, 1) == Y_test
accuracy = correct_prediction.float().mean()
print('Accuracy:', accuracy.item())
# Get one and predict
r = random.randint(0, len(mnist_test) - 1)
X_single_data = mnist_test.test_data[r:r + 1].view(-1, 28 * 28).float().to(device)
Y_single_data = mnist_test.test_labels[r:r + 1].to(device)
print('Label: ', Y_single_data.item())
single_prediction = model(X_single_data)
print('Prediction: ', torch.argmax(single_prediction, 1).item())
# Accuracy: 0.9765999913215637
# Label: 8
# Prediction: 3
Code : mnist_nn_deep
코스트 감소, 정답률 향상
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
import torch
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import random
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# for reproducibility
random.seed(777)
torch.manual_seed(777)
if device == 'cuda':
torch.cuda.manual_seed_all(777)
# parameters
learning_rate = 0.001
training_epochs = 15
batch_size = 100
# MNIST dataset
mnist_train = dsets.MNIST(root='MNIST_data/',
train=True,
transform=transforms.ToTensor(),
download=True)
mnist_test = dsets.MNIST(root='MNIST_data/',
train=False,
transform=transforms.ToTensor(),
download=True)
# dataset loader
data_loader = torch.utils.data.DataLoader(dataset=mnist_train,
batch_size=batch_size,
shuffle=True,
drop_last=True)
# nn layers
linear1 = torch.nn.Linear(784, 512, bias=True)
linear2 = torch.nn.Linear(512, 512, bias=True)
linear3 = torch.nn.Linear(512, 512, bias=True)
linear4 = torch.nn.Linear(512, 512, bias=True)
linear5 = torch.nn.Linear(512, 10, bias=True) # 레이어 추가
relu = torch.nn.ReLU()
# xavier initialization
torch.nn.init.xavier_uniform_(linear1.weight)
torch.nn.init.xavier_uniform_(linear2.weight)
torch.nn.init.xavier_uniform_(linear3.weight)
torch.nn.init.xavier_uniform_(linear4.weight)
torch.nn.init.xavier_uniform_(linear5.weight)
# model
model = torch.nn.Sequential(linear1, relu, linear2, relu, linear3).to(device)
# define cost/loss & optimizer
criterion = torch.nn.CrossEntropyLoss().to(device) # Softmax is internally computed.
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
total_batch = len(data_loader)
for epoch in range(training_epochs):
avg_cost = 0
for X, Y in data_loader:
# reshape input image into [batch_size by 784]
# label is not one-hot encoded
X = X.view(-1, 28 * 28).to(device)
Y = Y.to(device)
optimizer.zero_grad()
hypothesis = model(X)
cost = criterion(hypothesis, Y)
cost.backward()
optimizer.step()
avg_cost += cost / total_batch
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.9f}'.format(avg_cost))
print('Learning finished')
# Epoch: 0001 cost = 0.285469562
# Epoch: 0002 cost = 0.089996703
# Epoch: 0003 cost = 0.058415990
# Epoch: 0004 cost = 0.039738815
# Epoch: 0005 cost = 0.031502426
# Epoch: 0006 cost = 0.023690172
# Epoch: 0007 cost = 0.020800617
# Epoch: 0008 cost = 0.019785360
# Epoch: 0009 cost = 0.015893241
# Epoch: 0010 cost = 0.014122806
# Epoch: 0011 cost = 0.013081985
# Epoch: 0012 cost = 0.010510686
# Epoch: 0013 cost = 0.012267840
# Epoch: 0014 cost = 0.010862151
# Epoch: 0015 cost = 0.009223450
# Test the model using test sets
with torch.no_grad():
X_test = mnist_test.test_data.view(-1, 28 * 28).float().to(device)
Y_test = mnist_test.test_labels.to(device)
prediction = model(X_test)
correct_prediction = torch.argmax(prediction, 1) == Y_test
accuracy = correct_prediction.float().mean()
print('Accuracy:', accuracy.item())
# Get one and predict
r = random.randint(0, len(mnist_test) - 1)
X_single_data = mnist_test.test_data[r:r + 1].view(-1, 28 * 28).float().to(device)
Y_single_data = mnist_test.test_labels[r:r + 1].to(device)
print('Label: ', Y_single_data.item())
single_prediction = model(X_single_data)
print('Prediction: ', torch.argmax(single_prediction, 1).item())
# Accuracy: 0.9768999814987183
# Label: 8
# Prediction: 8
그 외 Weight initialization 방법
| 구분 | LeCun 초기화 (LeCun Initialization) | Orthogonal 초기화 (Orthogonal Initialization) | Batch Normalization 초기화 | LSUV 초기화 (Layer-sequential unit-variance Initialization) |
|---|---|---|---|---|
| 목적 | Sigmoid, Tanh 활성화 함수에서 안정적인 그래디언트 흐름 유지 | 가중치 행렬이 직교성을 유지하도록 초기화하여 정보 손실 방지 | 각 배치에서 입력을 정규화하여 층별로 안정적인 학습 제공 | 각 층의 출력이 초기 상태에서 단위 분산을 유지하여 학습 안정성 제공 |
| 특징 | 입력 노드 수에 비례하여 가중치 초기화 | 가중치 행렬이 직교 행렬로 설정되어 학습 중 정보 전파 시 손실이 없음 | 배치 단위로 입력을 정규화하여 출력의 분산을 일정하게 유지 | 각 층의 출력 분산을 단위 분산으로 조정하여 학습 초기에 빠른 수렴 유도 |
| 과정 | 입력 노드 수를 기준으로 가중치를 설정 | 직교 행렬을 생성하여 가중치 초기화 | 각 배치별 입력을 정규화하고 스케일링 및 시프팅을 통해 학습 과정에서 적용 | 초기 가중치를 설정한 후 각 층에서 출력 분산을 측정하고 단위 분산으로 조정 |
| 데이터 요구량 | 상대적으로 적음 | 상대적으로 적음 | 상대적으로 많음 | 상대적으로 적음 |
| 적합성 | Sigmoid, Tanh 활성화 함수를 사용하는 얕은 네트워크 | 순환 신경망(RNN), LSTM과 같은 깊은 네트워크에 적합 | 매우 깊은 네트워크(CNN, RNN 등)에서 신호 소실/폭주 방지 | CNN, DNN 등 다양한 네트워크에서 빠르고 안정적인 학습 수렴을 유도 |
This post is licensed under CC BY 4.0 by the author.