[모두를 위한 딥러닝 시즌2] Lab-09-4 Batch Normalization

Posted Nov 12, 2024

By 띵석

views 13 min read

Gradient Vanishing / Exploding

Gradient Vanishing
역전파 과정에서 입력층으로 갈수록 그라디언트가 너무 작아져 소멸하는 현상
Gradient Exploding
기울기가 입력층으로 갈수록 너무 큰 값이 되면서 발산되는 현상

해결책

Activate Function 변경
Weight initialization
Small learning rate
Batch Normalization (직접적인 방법)

Internal Covariate Shift

Covariate(공변량)이란 ?

데이터에서 결과 변수(종속 변수, Dependent Variable)에 영향을 미칠 가능성이 있는 독립 변수
- 어떤 시험 점수(결과 변수)에 영향을 미치는 공부 시간, 수면 시간, 집중도 등의 변수는 Covariates으로 간주될 수 있다
- 딥러닝에서는 입력 데이터의 각 특성(Feature)이 공변량 역할을 할 수 있다

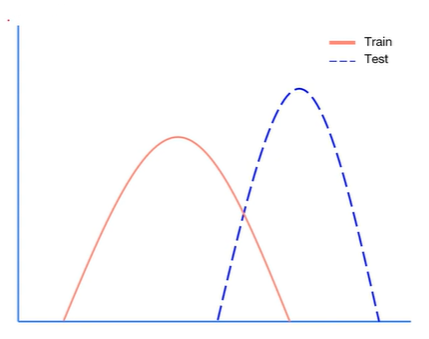
Covariate Shift

Train set과 Test set의 입력 특성(Feature) 분포가 다를 때 발생하는 문제
- 예시
- 훈련 데이터: 주간에 촬영된 도로 이미지 데이터를 사용해 자율주행 모델 훈련
- 테스트 데이터: 야간에 촬영된 도로 이미지 데이터
- 결과: 훈련 데이터에서 학습한 모델이 야간 테스트 데이터에서의 도로 및 차량 인식을 제대로 수행하지 못함
모델이 학습 데이터에는 잘 동작하지만 테스트 데이터에서는 성능이 저하될 가능성이 있음
Gradient Vanishing / Exploding을 야기함

Internal Covariate Shift

뉴럴 네트워크에서는 각 레이어를 통과할 때마다 입력 데이터를 처리하면서 출력 데이터의 분포가 변한다. 이러한 출력 데이터의 분포 변화를 Internal Covariate Shift라고 함
레이어가 깊어질수록 강도가 증가한다

예시 : 고양이 학습 과정

고양이 이미지가 여러 레이어를 통과하면서 점진적으로 더 추상화된 Feature로 변환
각 레이어마다 출력 데이터의 분포가 변화
레이어가 깊어질수록 Internal Covariate Shift가 강하게 발생

Batch Normalization

각 Layer마다 Normalization을 하는 Layer를 추가하여 Internal Covariate Shift를 해결할 수 있다.
mini-batch 마다 사용

작동 방식

Input

$B = {x_1, x_2, \dots, x_m}$: Mini-batch 내의 x 값
$\gamma\text{(Scale)}, \beta \text{(Shift Transform)}$: 학습 가능한 파라미터

Output

정규화 및 변환된 값: ${y_i = \text{BN}_{\gamma, \beta}(x_i)}$

Steps

Mini-batch mean(평균)
\[\mu_B \leftarrow \frac{1}{m} \sum_{i=1}^m x_i\]
Mini-batch variance(분산)
\[\sigma_B^2 \leftarrow \frac{1}{m} \sum_{i=1}^m (x_i - \mu_B)^2\]
Normalize
\[\hat{x}_i \leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\]
Scale and shift
\[y_i \leftarrow \gamma \hat{x}_i + \beta ≡ \text{BN}_{\gamma, \beta}(x_i)\]

Notes

$\epsilon$: 아주 작은 값으로, 0으로 나뉘는 현상을 방지하기 위해 추가
$\gamma, \beta$: Normalize 이후 활성화 함수의 Non-linearity 같은 성질을 잃게 되는 문제를 완화시켜준다. 역전파로 업데이트된다.
계산했던 sample mean(mini-batch mean), sample variance(mini-batch variance)를 따로 저장해두었다가 Sample mean 값들과, Sample variance 값들의 평균을 구해 Learning mean, Learning variance로 사용
- 즉, 최종적으로 모델을 inference할 때는 Learning mean, Learning variance를 사용한다.

학습 과정

초기 조건

Batch Normalization 파라미터 초기값:
- $\gamma = 1.0, \beta = 0.0$
- $\epsilon = 1 \times 10^{-5}$

Forward Pass (순전파)

Layer 1

입력 데이터
\[X_1 = \begin{bmatrix}\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix},\begin{bmatrix} 7 & 8 & 9 \\ 10 & 11 & 12 \end{bmatrix}\end{bmatrix}\]
Mini-batch 평균과 분산 계산
- 각 데이터 채널에 대해 평균($\mu_B$)과 분산($\sigma_B^2$) 계산
\[\mu_B = \begin{bmatrix} 4.5 & 6.5 & 8.5 \end{bmatrix}, \quad \sigma_B^2 = \begin{bmatrix} 8.25 & 8.25 & 8.25 \end{bmatrix}\]
데이터 정규화
- 평균과 분산을 사용해 입력 데이터를 정규화
\[\hat{X}_1 = \frac{X_1 - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} =\begin{bmatrix}\begin{bmatrix} -1.21 & -1.55 & -1.89 \\ -0.17 & -0.51 & -0.85 \end{bmatrix},\begin{bmatrix} 0.85 & 0.51 & 0.17 \\ 1.89 & 1.55 & 1.21 \end{bmatrix}\end{bmatrix}\]
스케일과 이동 적용
- 학습 가능한 파라미터 $\gamma = 1.0, \beta = 0.0$을 적용:
\[Y_1 = \gamma \hat{X}_1 + \beta = \hat{X}_1\]
ReLU 활성화 함수 적용
- 활성화 함수(ReLU)
\[Z_1 = \text{ReLU}(Y_1) =\begin{bmatrix}\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix},\begin{bmatrix} 0.85 & 0.51 & 0.17 \\ 1.89 & 1.55 & 1.21 \end{bmatrix}\end{bmatrix}\]

Layer 2

입력 데이터
\[X_2 = Z_1 =\begin{bmatrix}\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix},\begin{bmatrix} 0.85 & 0.51 & 0.17 \\ 1.89 & 1.55 & 1.21 \end{bmatrix}\end{bmatrix}\]
Mini-batch 평균과 분산 계산
\[\mu_B = \begin{bmatrix} 0.44 & 0.28 & 0.19 \end{bmatrix}, \quad\sigma_B^2 = \begin{bmatrix} 0.45 & 0.35 & 0.25 \end{bmatrix}\]
데이터 정규화
\[\hat{X}_2 = \frac{X_2 - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} =\begin{bmatrix}\begin{bmatrix} -0.66 & -0.47 & -0.38 \\ -0.66 & -0.47 & -0.38 \end{bmatrix},\begin{bmatrix} 0.62 & 0.39 & 0.22 \\ 1.07 & 0.92 & 0.80 \end{bmatrix}\end{bmatrix}\]
스케일과 이동 적용
- 초기값: $\gamma = 1.0, \beta = 0.0$
\[Y_2 = \gamma \hat{X}_2 + \beta = \hat{X}_2\]
ReLU 활성화 함수 적용
\[Z_2 = \text{ReLU}(Y_2) =\begin{bmatrix}\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix},\begin{bmatrix} 0.62 & 0.39 & 0.22 \\ 1.07 & 0.92 & 0.80 \end{bmatrix}\end{bmatrix}\]

Layer 3

입력 데이터
\[X_3 = Z_2 =\begin{bmatrix}\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix},\begin{bmatrix} 0.62 & 0.39 & 0.22 \\ 1.07 & 0.92 & 0.80 \end{bmatrix}\end{bmatrix}\]
Mini-batch 평균과 분산 계산
\[\mu_B = \begin{bmatrix} 0.42 & 0.26 \end{bmatrix}, \quad \sigma_B^2 = \begin{bmatrix} 0.30 & 0.20 \end{bmatrix}\]
데이터 정규화
\[\hat{X}_3 = \frac{X_3 - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} =\begin{bmatrix}\begin{bmatrix} -0.77 & -0.58 \\ -0.77 & -0.58 \end{bmatrix},\begin{bmatrix} 0.36 & 0.28 \\ 1.18 & 1.02 \end{bmatrix}\end{bmatrix}\]
스케일과 이동 적용
- 초기값: $\gamma = 0.8, \beta = -0.2$
\[Y_3 = \gamma \hat{X}_3 + \beta =\begin{bmatrix}\begin{bmatrix} -0.816 & -0.664 \\ -0.816 & -0.664 \end{bmatrix},\begin{bmatrix} 0.088 & 0.024 \\ 0.944 & 0.816 \end{bmatrix}\end{bmatrix}\]
ReLU 활성화 함수 적용
\[Z_3 = \text{ReLU}(Y_3) =\begin{bmatrix}\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix},\begin{bmatrix} 0.088 & 0.024 \\ 0.944 & 0.816 \end{bmatrix}\end{bmatrix}\]

Backward Pass (역전파)

손실 함수 계산
- Mean Squared Error (MSE)
\[L = \frac{1}{n} \sum (y_{\text{true}} - y_{\text{pred}})^2\]
Batch Normalization 파라미터 업데이트
- $\gamma$ 업데이트
\[\gamma_{\text{new}} = \gamma_{\text{old}} - \eta \cdot \frac{\partial L}{\partial \gamma}\]
- $\beta$ 업데이트
\[\beta_{\text{new}} = \beta_{\text{old}} - \eta \cdot \frac{\partial L}{\partial \beta}\]
가중치 업데이트
- 각 레이어의 가중치와 편향을 역전파를 통해 업데이트

주의점

Batch Normalization에서 $\gamma, \beta$ 값이 변경되지 않도록 model.eval()을 사용해야 한다

미니배치 크기에 의존적이다

드랍아웃, 배치 노말라이제이션을 항상 쓰면 결과가 안좋을 수 있다

Code : mnist_batchnorm

  
import torch
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pylab as plt
import matplotlib

device = "cuda" if torch.cuda.is_available() else "cpu"
matplotlib.use("tkagg")  # GUI 백엔드 설정

# for reproducibility
torch.manual_seed(1)
if device == "cuda":
    torch.cuda.manual_seed_all(1)
# parameters
learning_rate = 0.01
training_epochs = 10
batch_size = 32
# MNIST dataset
mnist_train = dsets.MNIST(
    root="MNIST_data/", train=True, transform=transforms.ToTensor(), download=True
)

mnist_test = dsets.MNIST(
    root="MNIST_data/", train=False, transform=transforms.ToTensor(), download=True
)
# dataset loader
train_loader = torch.utils.data.DataLoader(
    dataset=mnist_train, batch_size=batch_size, shuffle=True, drop_last=True
)

test_loader = torch.utils.data.DataLoader(
    dataset=mnist_test, batch_size=batch_size, shuffle=False, drop_last=True
)
# nn layers
linear1 = torch.nn.Linear(784, 32, bias=True)
linear2 = torch.nn.Linear(32, 32, bias=True)
linear3 = torch.nn.Linear(32, 10, bias=True)
relu = torch.nn.ReLU()
bn1 = torch.nn.BatchNorm1d(32)
bn2 = torch.nn.BatchNorm1d(32)

nn_linear1 = torch.nn.Linear(784, 32, bias=True)
nn_linear2 = torch.nn.Linear(32, 32, bias=True)
nn_linear3 = torch.nn.Linear(32, 10, bias=True)
# model
bn_model = torch.nn.Sequential(linear1, bn1, relu, linear2, bn2, relu, linear3).to(
    device
)
nn_model = torch.nn.Sequential(nn_linear1, relu, nn_linear2, relu, nn_linear3).to(
    device
)
# define cost/loss & optimizer
criterion = torch.nn.CrossEntropyLoss().to(device)  # Softmax is internally computed.
bn_optimizer = torch.optim.Adam(bn_model.parameters(), lr=learning_rate)
nn_optimizer = torch.optim.Adam(nn_model.parameters(), lr=learning_rate)

# Save Losses and Accuracies every epoch
# We are going to plot them later
train_losses = []
train_accs = []

valid_losses = []
valid_accs = []

train_total_batch = len(train_loader)
test_total_batch = len(test_loader)
for epoch in range(training_epochs):
    bn_model.train()  # set the model to train mode

    for X, Y in train_loader:
        # reshape input image into [batch_size by 784]
        # label is not one-hot encoded
        X = X.view(-1, 28 * 28).to(device)
        Y = Y.to(device)

        bn_optimizer.zero_grad()
        bn_prediction = bn_model(X)
        bn_loss = criterion(bn_prediction, Y)
        bn_loss.backward()
        bn_optimizer.step()

        nn_optimizer.zero_grad()
        nn_prediction = nn_model(X)
        nn_loss = criterion(nn_prediction, Y)
        nn_loss.backward()
        nn_optimizer.step()

    with torch.no_grad():
        bn_model.eval()  # set the model to evaluation mode

        # Test the model using train sets
        bn_loss, nn_loss, bn_acc, nn_acc = 0, 0, 0, 0
        for i, (X, Y) in enumerate(train_loader):
            X = X.view(-1, 28 * 28).to(device)
            Y = Y.to(device)

            bn_prediction = bn_model(X)
            bn_correct_prediction = torch.argmax(bn_prediction, 1) == Y
            bn_loss += criterion(bn_prediction, Y)
            bn_acc += bn_correct_prediction.float().mean()

            nn_prediction = nn_model(X)
            nn_correct_prediction = torch.argmax(nn_prediction, 1) == Y
            nn_loss += criterion(nn_prediction, Y)
            nn_acc += nn_correct_prediction.float().mean()

        bn_loss, nn_loss, bn_acc, nn_acc = (
            bn_loss / train_total_batch,
            nn_loss / train_total_batch,
            bn_acc / train_total_batch,
            nn_acc / train_total_batch,
        )

        # Save train losses/acc
        train_losses.append([bn_loss, nn_loss])
        train_accs.append([bn_acc, nn_acc])
        print(
            "[Epoch %d-TRAIN] Batchnorm Loss(Acc): bn_loss:%.5f(bn_acc:%.2f) vs No Batchnorm Loss(Acc): nn_loss:%.5f(nn_acc:%.2f)"
            % (
                (epoch + 1),
                bn_loss.item(),
                bn_acc.item(),
                nn_loss.item(),
                nn_acc.item(),
            )
        )
        # Test the model using test sets
        bn_loss, nn_loss, bn_acc, nn_acc = 0, 0, 0, 0
        for i, (X, Y) in enumerate(test_loader):
            X = X.view(-1, 28 * 28).to(device)
            Y = Y.to(device)

            bn_prediction = bn_model(X)
            bn_correct_prediction = torch.argmax(bn_prediction, 1) == Y
            bn_loss += criterion(bn_prediction, Y)
            bn_acc += bn_correct_prediction.float().mean()

            nn_prediction = nn_model(X)
            nn_correct_prediction = torch.argmax(nn_prediction, 1) == Y
            nn_loss += criterion(nn_prediction, Y)
            nn_acc += nn_correct_prediction.float().mean()

        bn_loss, nn_loss, bn_acc, nn_acc = (
            bn_loss / test_total_batch,
            nn_loss / test_total_batch,
            bn_acc / test_total_batch,
            nn_acc / test_total_batch,
        )

        # Save valid losses/acc
        valid_losses.append([bn_loss, nn_loss])
        valid_accs.append([bn_acc, nn_acc])
        print(
            "[Epoch %d-VALID] Batchnorm Loss(Acc): bn_loss:%.5f(bn_acc:%.2f) vs No Batchnorm Loss(Acc): nn_loss:%.5f(nn_acc:%.2f)"
            % (
                (epoch + 1),
                bn_loss.item(),
                bn_acc.item(),
                nn_loss.item(),
                nn_acc.item(),
            )
        )
        print()

print("Learning finished")
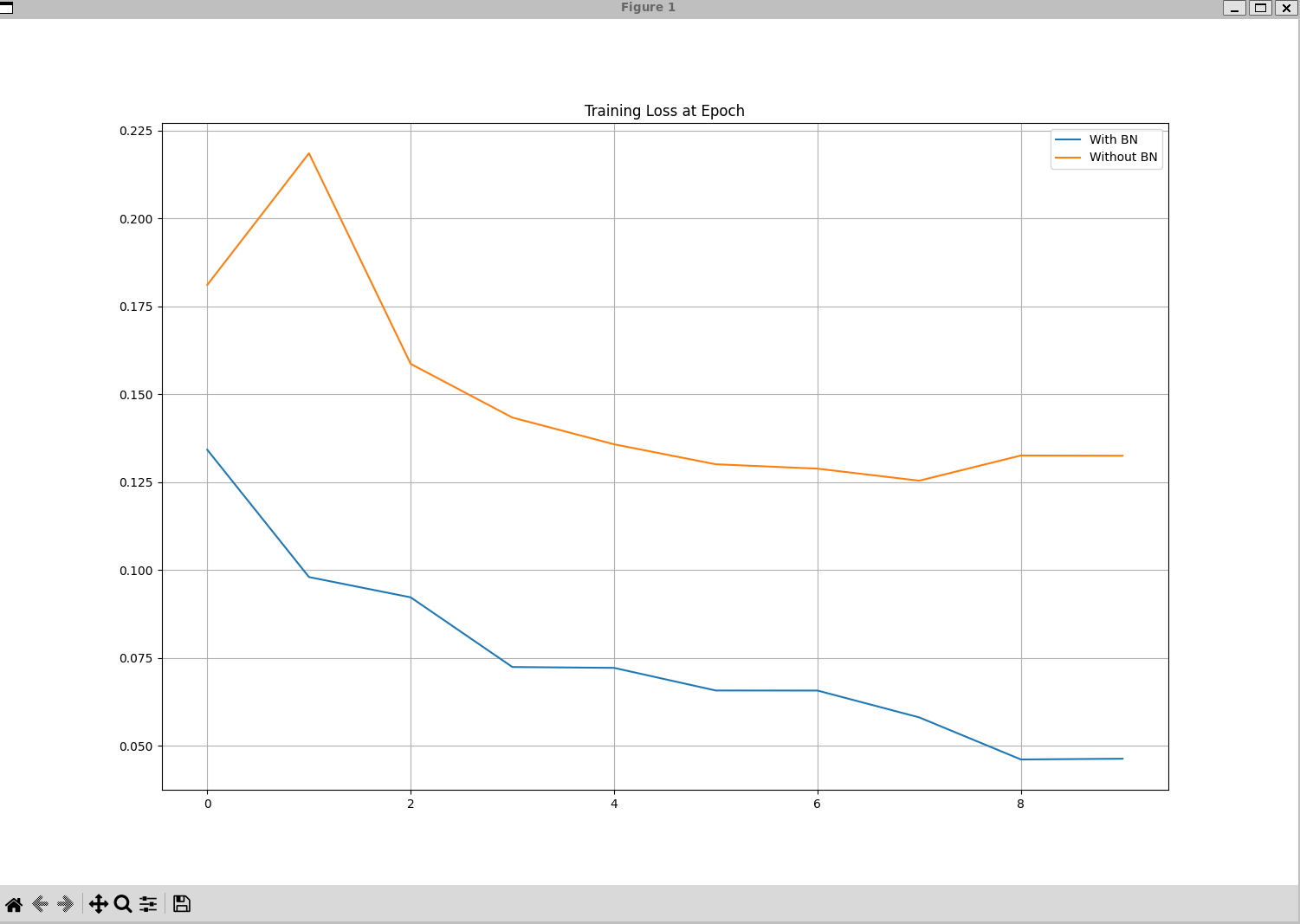
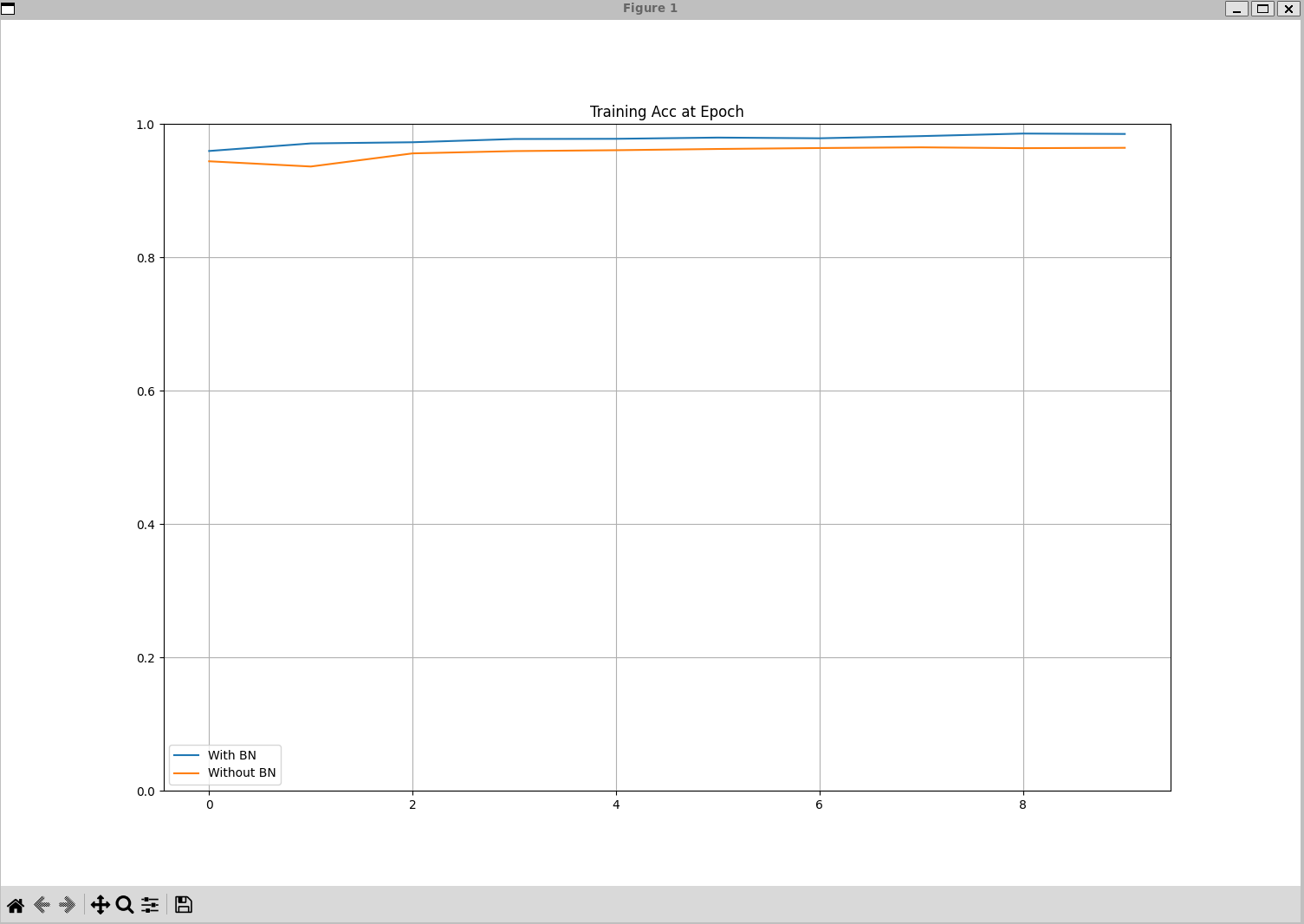
# [Epoch 1-TRAIN] Batchnorm Loss(Acc): bn_loss:0.13419(bn_acc:0.96) vs No Batchnorm Loss(Acc): nn_loss:0.18107(nn_acc:0.94)
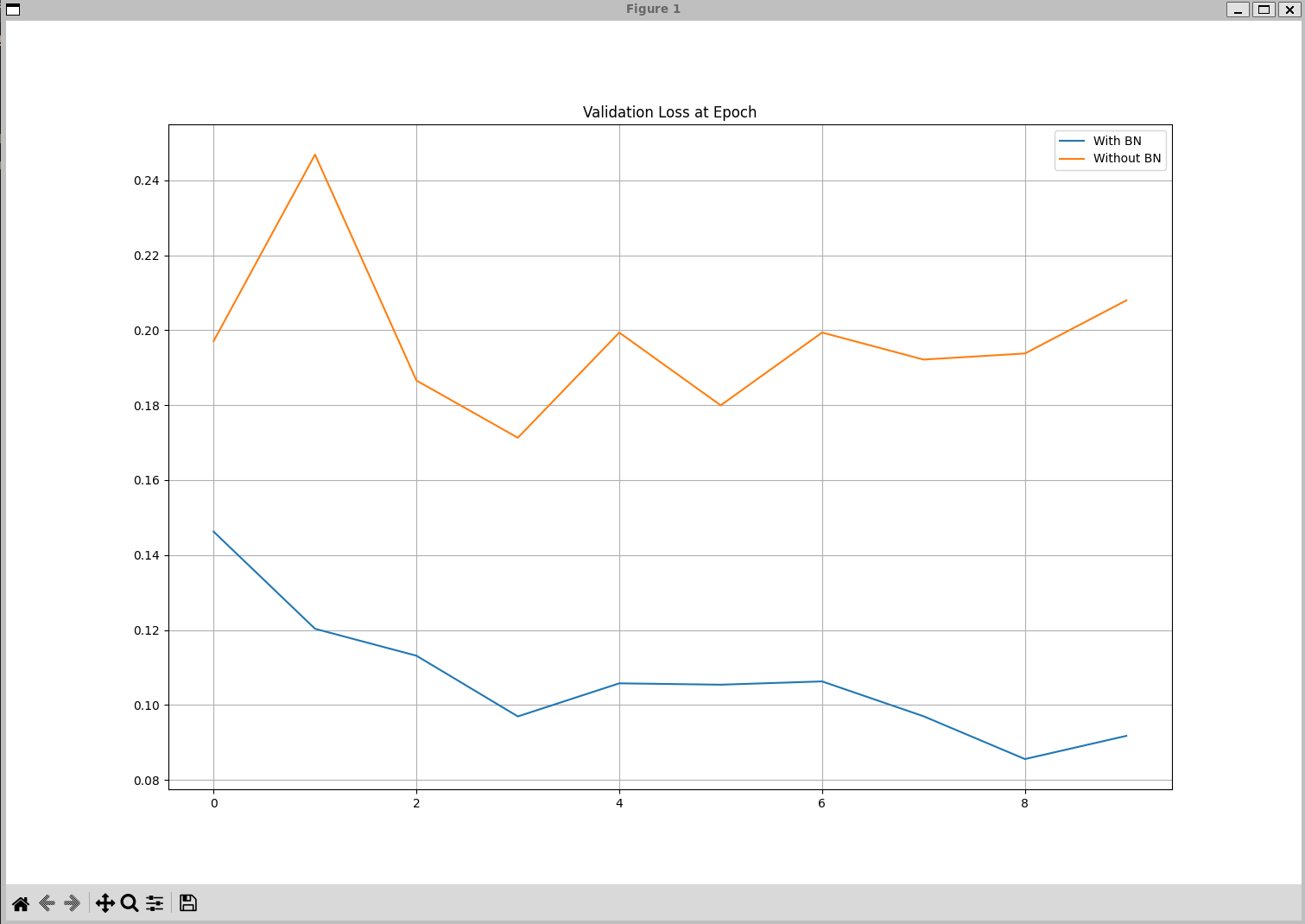
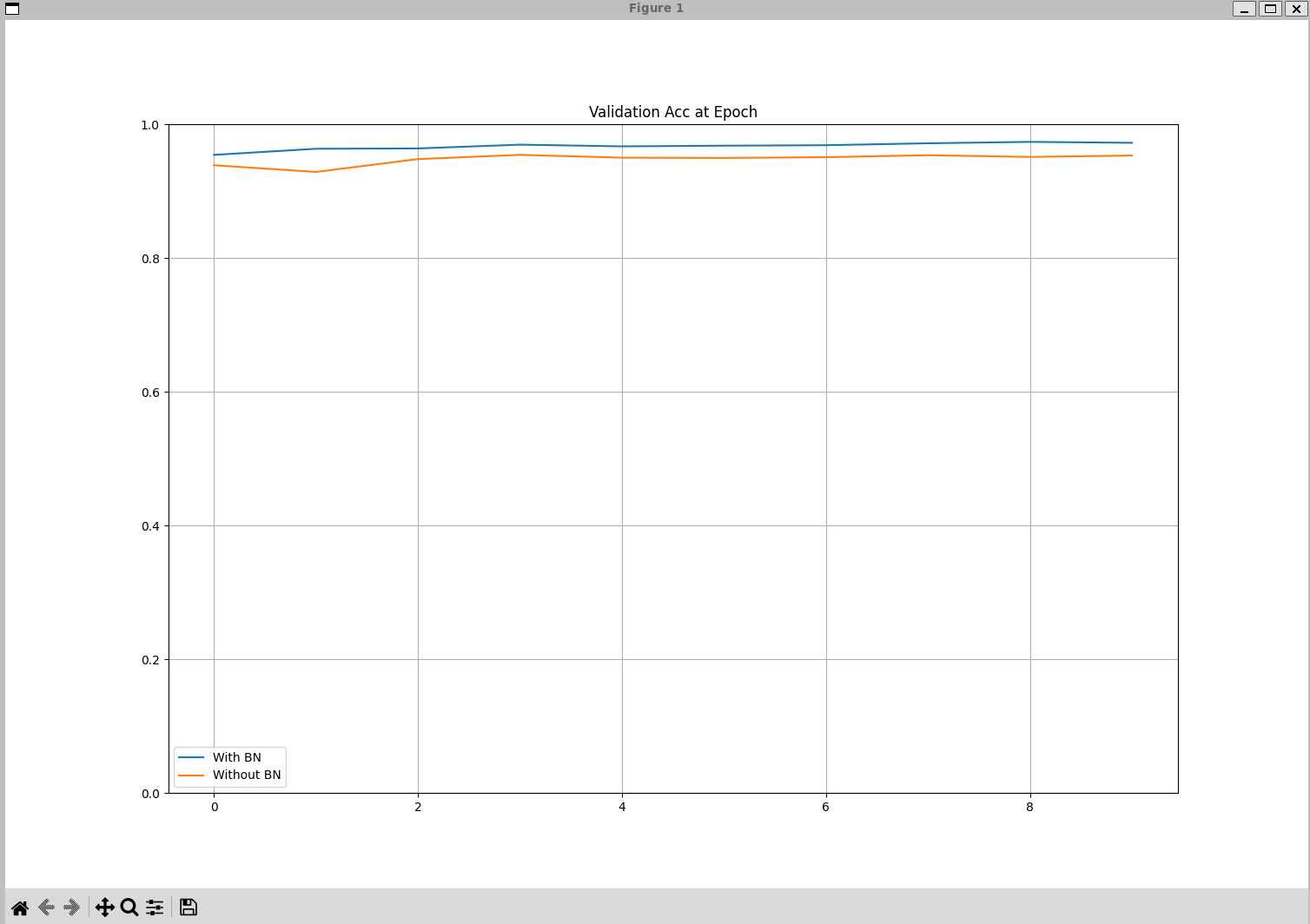
# [Epoch 1-VALID] Batchnorm Loss(Acc): bn_loss:0.14624(bn_acc:0.95) vs No Batchnorm Loss(Acc): nn_loss:0.19708(nn_acc:0.94)

# [Epoch 2-TRAIN] Batchnorm Loss(Acc): bn_loss:0.09798(bn_acc:0.97) vs No Batchnorm Loss(Acc): nn_loss:0.21851(nn_acc:0.94)
# [Epoch 2-VALID] Batchnorm Loss(Acc): bn_loss:0.12032(bn_acc:0.96) vs No Batchnorm Loss(Acc): nn_loss:0.24684(nn_acc:0.93)

# ...

# [Epoch 9-TRAIN] Batchnorm Loss(Acc): bn_loss:0.04610(bn_acc:0.99) vs No Batchnorm Loss(Acc): nn_loss:0.13256(nn_acc:0.96)
# [Epoch 9-VALID] Batchnorm Loss(Acc): bn_loss:0.08556(bn_acc:0.97) vs No Batchnorm Loss(Acc): nn_loss:0.19378(nn_acc:0.95)

# [Epoch 10-TRAIN] Batchnorm Loss(Acc): bn_loss:0.04632(bn_acc:0.98) vs No Batchnorm Loss(Acc): nn_loss:0.13249(nn_acc:0.96)
# [Epoch 10-VALID] Batchnorm Loss(Acc): bn_loss:0.09175(bn_acc:0.97) vs No Batchnorm Loss(Acc): nn_loss:0.20794(nn_acc:0.95)

def plot_compare(loss_list: list, ylim=None, title=None) -> None:
    # bn = [i[0] for i in loss_list]
    # nn = [i[1] for i in loss_list]
    # Convert tensors to NumPy arrays
    bn = [i[0].cpu().item() if torch.is_tensor(i[0]) else i[0] for i in loss_list]
    nn = [i[1].cpu().item() if torch.is_tensor(i[1]) else i[1] for i in loss_list]

    plt.figure(figsize=(15, 10))
    plt.plot(bn, label="With BN")
    plt.plot(nn, label="Without BN")
    if ylim:
        plt.ylim(ylim)

    if title:
        plt.title(title)
    plt.legend()
    plt.grid("on")
    plt.show()

plot_compare(train_losses, title="Training Loss at Epoch")
plot_compare(train_accs, [0, 1.0], title="Training Acc at Epoch")
plot_compare(valid_losses, title="Validation Loss at Epoch")
plot_compare(valid_accs, [0, 1.0], title="Validation Acc at Epoch")

오류 상황 : figurecanvasagg is non-interactive, and thus cannot be shown plt.show()

해결 방법

apt update
apt install python3-tk
코드 추가

  
import matplotlib
matplotlib.use("tkagg")

Study, AI

This post is licensed under CC BY 4.0 by the author.

Gradient Vanishing / Exploding

해결책

Internal Covariate Shift

Covariate(공변량)이란 ?

Covariate Shift

Internal Covariate Shift

Batch Normalization

작동 방식

학습 과정

초기 조건

Forward Pass (순전파)

Backward Pass (역전파)

주의점

Code : mnist_batchnorm

Trending Tags