[모두를 위한 딥러닝 시즌2] Lab-10-1 Convolution

Convolution

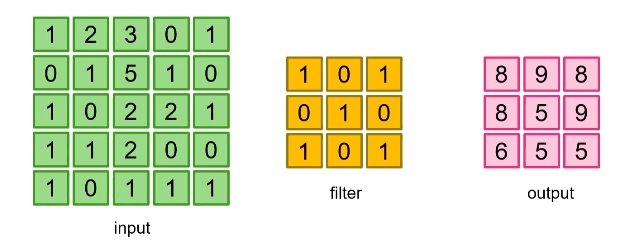
• 이미지 위에서 stride 값 만큼 filter(kernel)을 이동시키면서 겹쳐지는 부분의 각 원소의 값을 곱해서 모두 더한 값을 출력으로 하는 연산
• Stride와 Padding에 따라 출력 크기와 연산 영역이 달라진다
• Stride
  • filter가 연산 한 번에 이동하는 크기
  • 값이 커질수록 출력(Output) 크기가 작아진다
• padding
  • 입력(Input) 주변에 추가로 0(또는 다른 값)을 채워 넣는 작업
  • 주로 출력 크기를 조정하거나 경계 데이터 손실을 방지하기 위해 사용

Stride와 Padding 공식

\[\text{Output 크기} = \frac{\text{Input 크기} + 2 \cdot \text{Padding 크기} - \text{Filter 크기}}{\text{Stride}} + 1\]

계산 과정

• Input: 5x5 크기의 행렬
• Filter: 3x3 크기의 행렬
• Output: 3x3 크기의 행렬

---

1. Convolution 연산의 기본 개념

• Filter를 Input 행렬 위에서 슬라이딩하며 곱셈과 합산을 반복
• Filter와 Input이 겹치는 부분의 각 원소를 곱하고, 그 결과를 더하여 Output의 해당 위치에 값을 채워나감
• 이 과정은 Stride = 1(필터가 한 칸씩 이동) 기준으로 진행된다

---

2. 각 단계별 계산

(1) Output[0, 0]

Filter를 Input의 (0, 0) 위치에 겹쳐 계산

$Sum=(1⋅1)+(2⋅0)+(3⋅1)+(0⋅0)+(1⋅1)+(5⋅0)+(0⋅1)+(1⋅0)+(0⋅1)=8$

Output의 (0, 0)에 8 저장

(2) Output[0, 1]

Filter를 Input의 (0, 1) 위치에 겹쳐 계산

$Sum=(2⋅1)+(3⋅0)+(0⋅1)+(1⋅0)+(5⋅1)+(0⋅0)+(1⋅0)+(0⋅1)+(2⋅1)=9$

Output의 (0, 1)에 9 저장

…

위 과정을 반복

---

3. 최종 Output

Output 행렬 계산 결과

\[\text{Output} = \begin{bmatrix} 8 & 9 & 8 \\ 8 & 9 & 9 \\ 6 & 6 & 5 \end{bmatrix}\]

Pytorch nn.Conv2d

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, group=1, bias=True) 

• params
  • in_channels: input
  • out_channels: output
  • kernel_size: kernel사이즈 ex ) (2,4) (3,3) (4,3)
  • stride: stride 크기
  • padding: padding 크기
  • dilations(확장률): 필터의 요소 간 간격을 조정하는 데 사용됨
  • groups: 입력 및 출력 채널을 분할하여 Convolution 연산을 수행함
• 입력 형태
  • type : torch.Tensor
  • shape : (N x C x H x W) = (batch_size, channel, height, width)
• 예시 : 입력 채널 1 / 출력 채널 1 / 커널 크기 3x3 구현

conv = nn.Conv2d(1,1,3)

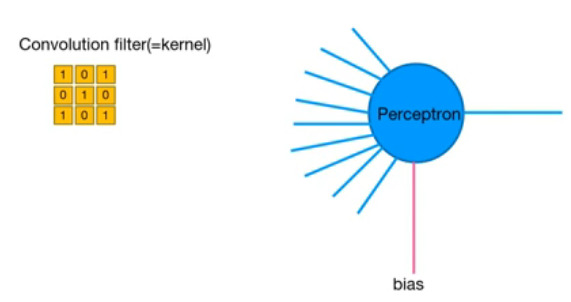
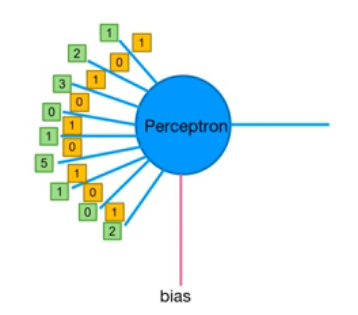
Neuron과 Convolution

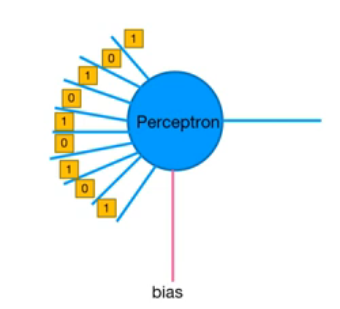
Perceptron과 Convolution 연산과정

1. filter와 Perceptron
   

2. Perceptron의 weight값으로 filter가 들어간다
   

3. Input data
   

4. 값과 가중치를 연결하여 연산한다
   

5. 결과 : \(1*1 + 2*0 + 3*1 + 0*0 +1*1 + 5*0 + 1*1 + 0*0 +2*1 + bias = 8 + bias\)

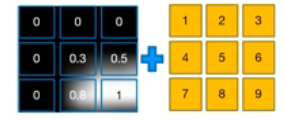
Pooling

• 이미지 사이즈를 줄임
• FC(Fully Connected) 연산을 대체하기 위해 Average Pooling 사용
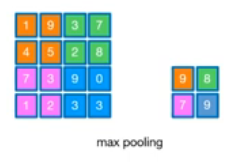
• Max Pooling : 해당 영역 내의 가장 큰 값을 선택

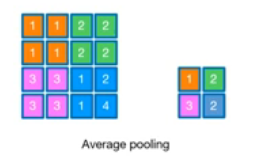
• Average Pooling : 해당 영역 내의 평균을 계산

MaxPool2d

torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False,ceil_mode=False)

• params
  • kernel_size: 커널 사이즈
  • 다른 값들은 default값이 존재하므로 커널 사이즈만 설정해도 된다

CNN implementation

import torch
import torch.nn as nn

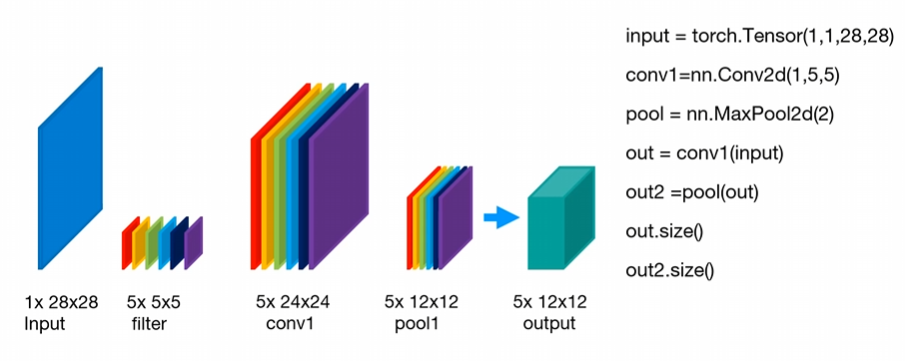
# 입력 텐서를 생성: 배치 크기 1, 채널 1, 높이 28, 너비 28
inputs = torch.Tensor(1, 1, 28, 28)  

# Conv2d 레이어 생성: 입력 채널 1, 출력 채널 5, 커널 크기 5
conv1 = nn.Conv2d(1, 5, 5)  

# MaxPool2d 레이어 생성: 커널 크기 2 (2x2 영역의 최대값 추출)
pool = nn.MaxPool2d(2)  

# Conv2d 레이어를 통과한 결과: 출력 채널 5, 크기 감소 (28x28 -> 24x24)
out = conv1(inputs)  

# MaxPool2d 레이어를 통과한 결과: 크기 감소 (24x24 -> 12x12)
out2 = pool(out)  

# Conv2d 레이어의 출력 크기 확인
out.size()  # torch.Size([1, 5, 24, 24])

# MaxPool2d 레이어의 출력 크기 확인
out2.size()  # torch.Size([1, 5, 12, 12])

Conv2d

\[\text{out}(N, C_{\text{out}}) = \text{bias}(C_{\text{out}}) + \sum_{k=0}^{C_{\text{in}}-1} \text{weight}(C_{\text{out}}, k) \star \text{input}(N, k)\]

• 필터(Filter)와 입력 이미지(Input)의 겹침 정도를 계산하여 출력(Output)을 생성

Convolution과 Cross-Correlation의 차이

Convolution (컨볼루션)

\[G'[i, j] = H \ast H' = \sum_{u=-\infty}^{\infty} \sum_{v=-\infty}^{\infty} H[i - u, j - v] F[u, v]\]

• 필터 $H′$가 뒤집힌 상태에서 입력 $F$와의 연산을 수행
• 흔히 신호 처리와 딥러닝에서 사용하는 핵심 연산으로, 필터의 방향성과 형태를 고려하여 계산

Cross-Correlation (교차상관)

\[T[i, j] = H \otimes K = \sum_{u=-\infty}^{\infty} \sum_{v=-\infty}^{\infty} H[i + u, j + v] K[u, v]\]

• 필터 $K$가 뒤집히지 않은 상태에서 입력과 연산을 수행
• 겹침의 정도를 계산하여 출력 값을 생성하며, 딥러닝에서 대부분의 “컨볼루션” 연산은 실제로 Cross-correlation에 해당

---

Cross-correlation 특징

• Cross-correlation은 입력 요소들의 가중합(Weighted sum)을 기반으로 출력 값을 생성
• 이때 필터(Filter)는 뒤집히지 않은 상태로 입력과 연산
• 딥러닝에서 Conv2d 연산은 Cross-correlation 방식으로 동작하지만 “Convolution”이라는 이름을 사용

---

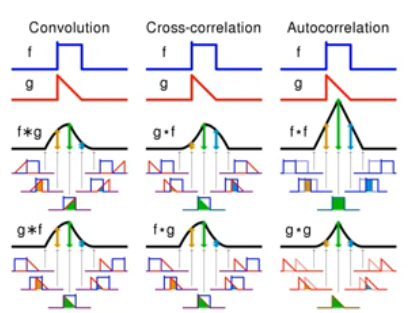
시각적 비교

• Convolution: 필터가 입력 위에서 뒤집혀 작동
• Cross-correlation: 필터가 뒤집히지 않은 상태에서 입력을 스캔
• Autocorrelation: 동일한 신호끼리의 유사도를 계산