[모두를 위한 딥러닝 시즌2] Lab-11-2 RNN hihello and charseq
[모두를 위한 딥러닝 시즌2] Lab-11-2 RNN hihello and charseq
“ Hihello” problem
- hihello 문자열 예측
- ‘h’ → ‘i’ 예측, ‘i’ → ‘h’ 예측 → ‘h’ → ‘e’ 예측, ‘e’ → ‘l’ 예측, ‘l’ → ‘l’예측, ‘l’ → ‘o’ 예측
- character에 따라 다음 character를 예측
- 다른 char들은 하나라서 예측이 쉽지만, ‘h’ 가 들어오면 ‘e’, ‘i’ 가 될 수도있고, ‘l’ 가 들어오면 ‘l’, ‘o’ 가 될 수 있음 → 하나의 문자에 대한 예측은 다양한 가능성을 내포하고 있음
- 따라서 모델이 어디까지 진행된 상태인지 저장되는 RNN의 hidden state 역할이 중요함
- 현재 입력뿐만 아니라 이전 시점의 hidden state 정보를 포함
- 입력이 동일하더라도 문맥에 따라 다른 출력을 생성할 수 있도록 함
Data setting
index로 표현
- 가장 쉬운 방법
- ‘h’ → 0
- ‘i’ → 1
- ‘e’ → 2
- ‘l’ → 3
- ‘o’ → 4
- 단순히 인덱스를 매길 경우, 숫자의 크기에 따라 의미 부여가 될 수 있음
'o' → 4와'h' → 0사이의 차이가 크다고 인식'l' → 3이'i' → 1보다 더 큰 중요성을 가진다고 인식
- Continuous하지 않고 categorical 데이터를 표현할 때는 주로 one-hot encoding을 사용
1
char_set = ['h', 'i', 'e', 'l', 'o']
one-hot encoding
- 벡터의 한 축에서만 1로 표현되고, 나머지는 0으로 표현되는 방식
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
char_set = ['h', 'i', 'e', 'l', 'o']
# character에 따라 다음 character를 예측
# 입력 데이터: 'hihell'을 인덱스로 표현
# 'h' -> 0, 'i' -> 1, 'h' -> 0, 'e' -> 2, 'l' -> 3, 'l' -> 3
x_data = [[0, 1, 0, 2, 3, 3]]
# 각 인덱스를 원-핫 벡터로 변환
x_one_hot = [
[[1, 0, 0, 0, 0], # 'h' -> [1, 0, 0, 0, 0]
[0, 1, 0, 0, 0], # 'i' -> [0, 1, 0, 0, 0]
[1, 0, 0, 0, 0], # 'h' -> [1, 0, 0, 0, 0]
[0, 0, 1, 0, 0], # 'e' -> [0, 0, 1, 0, 0]
[0, 0, 0, 1, 0], # 'l' -> [0, 0, 0, 1, 0]
[0, 0, 0, 1, 0]] # 'l' -> [0, 0, 0, 1, 0]
]
# 출력 데이터: 'ihello'를 인덱스로 표현
# 'i' -> 1, 'h' -> 0, 'e' -> 2, 'l' -> 3, 'l' -> 3, 'o' -> 4
y_data = [[1, 0, 2, 3, 3, 4]]
Cross entropy loss
- 카테고리 예측 모델에서 일반적으로 사용되는 손실 함수
- 카테고리 예측 모델은 소프트맥스 모델을 이용해 확률 값을 예상함
- 예상한 확률 값을 최대화하여, 정답 레이블에 최대한 가깝도록 조정하는 역할
- 내부적으로 소프트맥스를 적용
1
2
3
4
5
6
7
criterion = torch.nn.CrossEntropyLoss()
...
loss = criterion(outputs.view(-1, input_size), Y.view(-1))
# RNN의 출력은 (batch_size, sequence_length, input_size) 형태
# CrossEntropyLoss는 (N, C) 형태의 입력을 요구
# N = batch_size × sequence_length (전체 데이터 포인트 수)
# C = input_size (클래스 수)
- 파이토치에서는 손실 함수를 정의하기 위해 두 개의 파라미터를 사용
- 첫 번째 파라미터는 모델의 아웃풋
- 두 번째는 정답 레이블
- 만약 파라미터의 순서를 잘못 설정하면 모델이 제대로 동작하지 않을 수 있다
Code run through (hihello)
- hidden_size
- RNN이 각 시점에서 생성하는 hidden state의 차원
- input_size와 같지 않아도 된다
- 기억 용량 또는 표현력을 조정하는 데 사용
input_size=5, hidden_size=10: 더 많은 기억 용량을 제공 (더 큰 표현력)input_size=5, hidden_size=3: 더 작은 모델로 효율성 증대- Hidden Size가 클수록 모델은 더 많은 패턴과 정보를 학습 가능. 하지만 너무 크게 설정하면 overfitting이 발생하거나 계산 비용 증가
- 입력 데이터(X)는 FloatTensor로 변환되며, 이는 RNN의 연산에 적합
- 출력 데이터(Y)는 LongTensor로 변환되며, CrossEntropyLoss에서 레이블 데이터로 사용
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
import torch
import torch.optim as optim
import numpy as np
torch.manual_seed(0)
# 문자 집합 정의
char_set = ['h', 'i', 'e', 'l', 'o']
# 하이퍼파라미터 설정
input_size = len(char_set) # 입력의 크기 (문자 집합의 크기)
hidden_size = len(char_set) # 은닉 상태의 크기
learning_rate = 0.1
# 데이터 설정
# 입력 데이터: 'hihell'을 인덱스로 표현
x_data = [[0, 1, 0, 2, 3, 3]]
# 입력 데이터의 원-핫 인코딩 표현
x_one_hot = [[[1, 0, 0, 0, 0], # 'h'
[0, 1, 0, 0, 0], # 'i'
[1, 0, 0, 0, 0], # 'h'
[0, 0, 1, 0, 0], # 'e'
[0, 0, 0, 1, 0], # 'l'
[0, 0, 0, 1, 0]]] # 'l'
# 출력 데이터: 'ihello'를 인덱스로 표현
y_data = [[1, 0, 2, 3, 3, 4]]
# 데이터를 PyTorch 텐서로 변환
X = torch.FloatTensor(x_one_hot)
Y = torch.LongTensor(y_data)
# RNN 모델 선언
# batch_first=True로 설정하여 입력 데이터의 첫 번째 차원이 배치 크기임을 명시
rnn = torch.nn.RNN(input_size, hidden_size, batch_first=True) # batch_first guarantees the order of output = (B, S, F)
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.Adam(rnn.parameters(), learning_rate)
# 학습 시작
for i in range(100):
optimizer.zero_grad()
outputs, _status = rnn(X) # RNN에 입력 데이터 전달하여 출력과 상태 반환
# 출력 텐서를 2차원으로 변환하여 손실 계산
loss = criterion(outputs.view(-1, input_size), Y.view(-1))
loss.backward()
optimizer.step()
# 예측 결과를 numpy 배열로 변환하여 최종 예측 값 도출
result = outputs.data.numpy().argmax(axis=2)
# 예측 인덱스를 문자로 변환하여 문자열 생성
result_str = ''.join([char_set[c] for c in np.squeeze(result)])
print(i, "loss: ", loss.item(), "prediction: ", result, "true Y: ", y_data, "prediction str: ", result_str)
# 0 loss: 1.7802648544311523 prediction: [[1 1 1 1 1 1]] true Y: [[1, 0, 2, 3, 3, 4]] prediction str: iiiiii
# 1 loss: 1.4931949377059937 prediction: [[1 4 1 1 4 4]] true Y: [[1, 0, 2, 3, 3, 4]] prediction str: ioiioo
# 2 loss: 1.3337111473083496 prediction: [[1 3 2 3 1 4]] true Y: [[1, 0, 2, 3, 3, 4]] prediction str: ilelio
# 3 loss: 1.215294599533081 prediction: [[2 3 2 3 3 3]] true Y: [[1, 0, 2, 3, 3, 4]] prediction str: elelll
# 4 loss: 1.1131387948989868 prediction: [[2 3 2 3 3 3]] true Y: [[1, 0, 2, 3, 3, 4]] prediction str: elelll
# ...
# 96 loss: 0.5322802662849426 prediction: [[1 3 2 3 3 4]] true Y: [[1, 0, 2, 3, 3, 4]] prediction str: ilello
# 97 loss: 0.5321123600006104 prediction: [[1 3 2 3 3 4]] true Y: [[1, 0, 2, 3, 3, 4]] prediction str: ilello
# 98 loss: 0.5319532752037048 prediction: [[1 3 2 3 3 4]] true Y: [[1, 0, 2, 3, 3, 4]] prediction str: ilello
# 99 loss: 0.5317899584770203 prediction: [[1 3 2 3 3 4]] true Y: [[1, 0, 2, 3, 3, 4]] prediction str: ilello
Code run through (charseq)
- hihello 의 data를 일반화한 코드
- np.eye
- 원-핫 인코딩 벡터를 간단히 생성
np.eye(dic_size)[x]: x에 해당하는 인덱스 위치만 1이고 나머지는 0인 원-핫 벡터를 생성
1 2 3 4 5 6
dic_size=5 x=[0, 1, 2] np.eye(5)[x] = [[1, 0, 0, 0, 0], # 0 -> 'h' [0, 1, 0, 0, 0], # 1 -> 'i' [0, 0, 1, 0, 0]] # 2 -> 'e'
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import torch
import torch.optim as optim
import numpy as np
torch.manual_seed(0)
# 예제 문자열
sample = " if you want you"
# 문자 집합 정의
char_set = list(set(sample)) # 문자열의 중복을 제거하여 문자 집합 생성
char_dic = {c: i for i, c in enumerate(char_set)} # 문자에 인덱스를 매핑한 딕셔너리 생성
# 하이퍼파라미터 설정
dic_size = len(char_dic) # 입력의 크기 (문자 집합의 크기)
hidden_size = len(char_dic) # 은닉 상태의 크기
learning_rate = 0.1
# 데이터 설정
# 입력 문자열을 인덱스로 변환
sample_idx = [char_dic[c] for c in sample] # 문자열의 각 문자를 대응되는 인덱스로 변환
x_data = [sample_idx[:-1]] # 입력 데이터는 마지막 문자를 제외한 부분
x_one_hot = [np.eye(dic_size)[x] for x in x_data] # 입력 데이터를 원-핫 인코딩으로 변환
y_data = [sample_idx[1:]] # 출력 데이터는 첫 번째 문자를 제외한 부분
# 데이터를 PyTorch 텐서로 변환
X = torch.FloatTensor(x_one_hot)
Y = torch.LongTensor(y_data)
# RNN 모델 선언
# batch_first=True로 설정하여 입력 데이터의 첫 번째 차원이 배치 크기임을 명시
rnn = torch.nn.RNN(dic_size, hidden_size, batch_first=True) # batch_first guarantees the order of output = (B, S, F)
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.Adam(rnn.parameters(), learning_rate)
# 학습 시작
for i in range(100):
optimizer.zero_grad()
outputs, _status = rnn(X) # RNN에 입력 데이터 전달하여 출력과 상태 반환
# 출력 텐서를 2차원으로 변환하여 손실 계산
loss = criterion(outputs.view(-1, dic_size), Y.view(-1))
loss.backward()
optimizer.step()
# 예측 결과를 numpy 배열로 변환하여 최종 예측 값 도출
result = outputs.data.numpy().argmax(axis=2)
# 예측 인덱스를 문자로 변환하여 문자열 생성
result_str = ''.join([char_set[c] for c in np.squeeze(result)])
print(i, "loss: ", loss.item(), "prediction: ", result, "true Y: ", y_data, "prediction str: ", result_str)
# 0 loss: 2.342663288116455 prediction: [[8 7 7 8 5 0 0 8 7 0 8 5 8 5 0]] true Y: [[4, 3, 2, 0, 7, 9, 2, 5, 1, 8, 6, 2, 0, 7, 9]] prediction str: noonwyynoynwnwy
# 1 loss: 2.005516529083252 prediction: [[8 7 2 8 7 0 0 8 7 2 7 2 8 7 0]] true Y: [[4, 3, 2, 0, 7, 9, 2, 5, 1, 8, 6, 2, 0, 7, 9]] prediction str: no noyyno o noy
# 2 loss: 1.7695480585098267 prediction: [[8 7 2 0 7 9 0 5 7 2 7 2 0 7 9]] true Y: [[4, 3, 2, 0, 7, 9, 2, 5, 1, 8, 6, 2, 0, 7, 9]] prediction str: no youywo o you
# 3 loss: 1.5684891939163208 prediction: [[5 7 2 0 7 9 2 5 1 9 7 2 0 7 9]] true Y: [[4, 3, 2, 0, 7, 9, 2, 5, 1, 8, 6, 2, 0, 7, 9]] prediction str: wo you wauo you
# 4 loss: 1.4520589113235474 prediction: [[5 3 2 0 7 9 2 5 1 9 6 2 0 7 9]] true Y: [[4, 3, 2, 0, 7, 9, 2, 5, 1, 8, 6, 2, 0, 7, 9]] prediction str: wf you waut you
# ...
# 96 loss: 0.8099259734153748 prediction: [[4 3 2 0 7 9 2 5 1 8 6 2 0 7 9]] true Y: [[4, 3, 2, 0, 7, 9, 2, 5, 1, 8, 6, 2, 0, 7, 9]] prediction str: if you want you
# 97 loss: 0.8098456263542175 prediction: [[4 3 2 0 7 9 2 5 1 8 6 2 0 7 9]] true Y: [[4, 3, 2, 0, 7, 9, 2, 5, 1, 8, 6, 2, 0, 7, 9]] prediction str: if you want you
# 98 loss: 0.8097667694091797 prediction: [[4 3 2 0 7 9 2 5 1 8 6 2 0 7 9]] true Y: [[4, 3, 2, 0, 7, 9, 2, 5, 1, 8, 6, 2, 0, 7, 9]] prediction str: if you want you
# 99 loss: 0.8096891045570374 prediction: [[4 3 2 0 7 9 2 5 1 8 6 2 0 7 9]] true Y: [[4, 3, 2, 0, 7, 9, 2, 5, 1, 8, 6, 2, 0, 7, 9]] prediction str: if you want you
Code run through
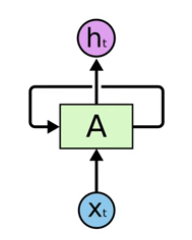
RNN 내부 연산 구조
은닉 상태 업데이트 ($h_t$)
- 이전 시점의 은닉 상태 $h_{t-1}$와 현재 입력 $x_t$를 결합하여 계산
- 공식 $h_t = \tanh(W_h \cdot h_{t-1} + W_x \cdot x_t + b)$
- $W_h$: 은닉 상태의 가중치 행렬
- $W_x$: 입력 데이터의 가중치 행렬
- $b$: 편향 값
- $\tanh$: 활성화 함수 (하이퍼볼릭 탄젠트)
Time Step ($t$)별 연산
| Time Step ($t$) | Input ($x_t$) | Previous Hidden ($h_{t-1})$ | Current Hidden ($h_t$) | Prediction ($y_t$) |
|---|---|---|---|---|
| 1 | ’ ‘ | $h_0 = 0$ | $h_1 = \tanh(W_x \cdot x_1 + b)$ | ‘i’ |
| 2 | ‘i’ | $h_1$ | $h_2 = \tanh(W_h \cdot h_1 + W_x \cdot x_2 + b)$ | ‘f’ |
| 3 | ‘f’ | $h_2$ | $h_3 = \tanh(W_h \cdot h_2 + W_x \cdot x_3 + b)$ | ’ ‘ |
| 4 | ’ ‘ | $h_3$ | $h_4 = \tanh(W_h \cdot h_3 + W_x \cdot x_4 + b)$ | ‘y’ |
| 5 | ‘y’ | $h_4$ | $h_5 = \tanh(W_h \cdot h_4 + W_x \cdot x_5 + b)$ | ‘o’ |
| … | … | … | … | … |
| $T$ | ‘u’ | $h_{T-1}$ | $h_T = \tanh(W_h \cdot h_{T-1} + W_x \cdot x_T + b)$ | ’ ‘ |
This post is licensed under CC BY 4.0 by the author.