[모두를 위한 딥러닝 시즌2] Lab-11-4 RNN timeseries

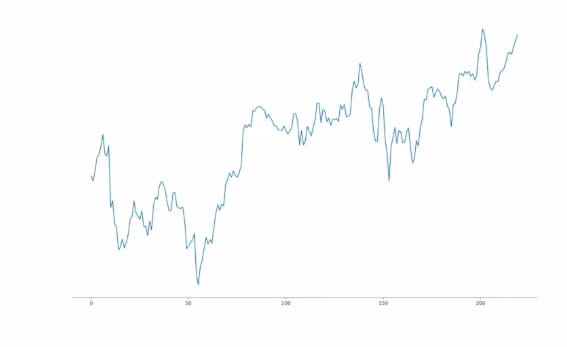
Time Series Data

• 시계열 데이터
• 일정 시간 간격으로 배치된 데이터
• 예) 주가 데이터

Apply RNN

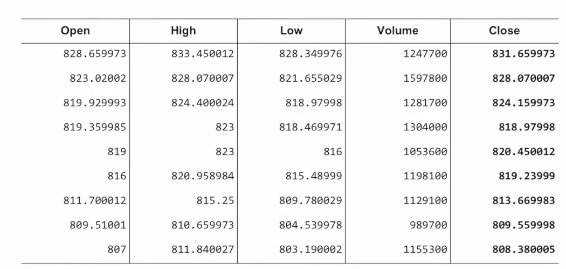
• 일별 구글 주가 데이터

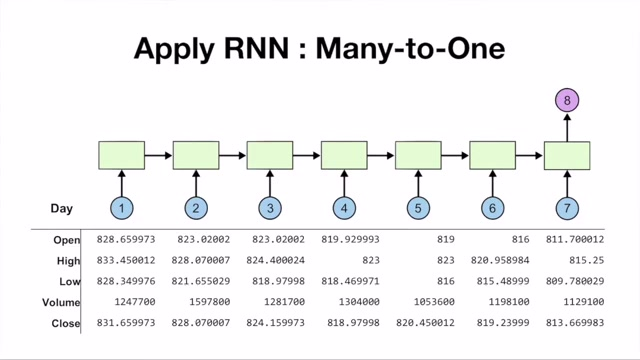
Many-to-One

• 7일간의 데이터를 입력받아서 8일 차 종가 예측을 하는 모델

• 모델은 8일 차 종가 예측을 위해 일주일 간의 데이터를 사용한다는 전제를 기반으로 작동

  → 주식 시장의 다양한 가정들로 인해 정확한 예측은 불가능하다

• 입력 데이터: 이전 7일간의 주가 데이터 (5개 요소: 시가, 종가, 최고가, 최저가, 거래량)
• 출력 데이터: 8일 차의 종가

이 네트워크가 8일 차의 종가를 바로 맞춘다면?

• 각 셀에서 나오는 아웃풋은 하나의 값만 가지게 된다(dim = 1)

• 이전에 데이터를 통합하기 위한 모든 단계에서의 hidden state도 차원이 한개만 가지게 된다

  → 입력 데이터 5개를 처리, 결과를 종합하고 압축하여 전달해줘야 함

• 이는 모델에게 매우 부담스러운 작업
• 따라서, 일반적으로는 데이터를 유통하기 위한 hidden state의 차원을 충분히 보장해주고, 유통되어서 마지막 출력 단계에서 FC layer를 연결하여 아웃풋을 예측하도록 함
• 데이터를 유통하는 부분과 예측하는 부분을 분리하여 네트워크의 부담을 분산시키는 것이 중요하다

Data Reading

• 데이터를 시간 순서대로 처리하기 위해 역순으로 정렬
• 주가와 거래량의 값 범위 차이가 크기 때문에 모델 학습의 부담을 줄이기 위해 데이터를 0과 1 사이 값으로 정규화
  • 최솟값과 최댓값을 기준으로 선형 변환
• 70%는 학습 데이터로, 30%는 테스트 데이터로 사용

import torch
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt

# 랜덤 시드 설정
torch.manual_seed(0)

# 데이터 스케일링 함수 (0과 1 사이로 정규화)
def minmax_scaler(data):
    numerator = data - np.min(data, 0)  # 각 열에서 최솟값을 뺌
    denominator = np.max(data, 0) - np.min(data, 0)  # 각 열의 범위를 계산
    return numerator / (denominator + 1e-7)  # 1e-7을 더해 나눗셈 에러 방지

# 데이터셋 생성 함수
def build_dataset(time_series, seq_length):
    dataX = []  # 입력 데이터 (X)
    dataY = []  # 출력 데이터 (Y)
    for i in range(0, len(time_series) - seq_length):
        _x = time_series[i:i + seq_length, :]  # 시퀀스 길이만큼 데이터를 자름
        _y = time_series[i + seq_length, [-1]]  # 다음 날의 종가를 예측
        print(_x, "->", _y)
        dataX.append(_x)  # 입력 데이터 추가
        dataY.append(_y)  # 출력 데이터 추가
    return np.array(dataX), np.array(dataY)

# 하이퍼파라미터 설정
seq_length = 7  # 시퀀스 길이 (7일)
data_dim = 5  # 입력 데이터 차원 (시가, 고가, 저가, 종가, 거래량)
hidden_dim = 10  # LSTM 히든 노드 개수
output_dim = 1  # 출력 차원 (종가)
learning_rate = 0.01  # 학습률
iterations = 500  # 학습 반복 횟수

# 데이터 로드
xy = np.loadtxt("data-02-stock_daily.csv", delimiter=",")  # CSV 파일에서 데이터 로드
xy = xy[::-1]  # 데이터를 시간 순서대로 정렬 (역순)

# 학습 데이터와 테스트 데이터로 분리
train_size = int(len(xy) * 0.7)  # 학습 데이터는 전체의 70%
train_set = xy[0:train_size]  # 학습 데이터
test_set = xy[train_size - seq_length:]  # 테스트 데이터 (시퀀스 길이를 고려)

# 데이터 스케일링 (0과 1 사이로 정규화)
train_set = minmax_scaler(train_set)
test_set = minmax_scaler(test_set)

# 학습 데이터와 테스트 데이터셋 생성
trainX, trainY = build_dataset(train_set, seq_length)
testX, testY = build_dataset(test_set, seq_length)

# 텐서로 변환 (PyTorch가 처리할 수 있는 형식)
trainX_tensor = torch.FloatTensor(trainX)
trainY_tensor = torch.FloatTensor(trainY)
testX_tensor = torch.FloatTensor(testX)
testY_tensor = torch.FloatTensor(testY)

Neural Net Setting

• LSTM Layer
  • 시계열 데이터를 처리하기 위해 사용
  • 입력 데이터의 각 시퀀스를 처리하며, 히든 상태를 유지하여 정보를 전달
• Fully Connected Layer
  • LSTM의 마지막 시점 출력만 사용하여 Fully Connected Layer를 통해 최종 출력값(종가)을 예측

# LSTM 모델 정의
class Net(torch.nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, layers):
        super(Net, self).__init__()
        self.rnn = torch.nn.LSTM(input_dim, hidden_dim, num_layers=layers, batch_first=True)  # LSTM 레이어
        self.fc = torch.nn.Linear(hidden_dim, output_dim, bias=True)  # Fully Connected Layer

    def forward(self, x):
        x, _status = self.rnn(x)  # LSTM 출력
        x = self.fc(x[:, -1])  # 마지막 시점의 출력만 사용
        return x

# 모델 초기화
net = Net(data_dim, hidden_dim, output_dim, 1)

# 손실 함수와 옵티마이저 설정
criterion = torch.nn.MSELoss()  # 손실 함수: 평균 제곱 오차(MSE)
optimizer = optim.Adam(net.parameters(), lr=learning_rate)  # 옵티마이저: Adam

Training & Evalutaion

# 모델 학습
for i in range(iterations):
    optimizer.zero_grad()  # 기울기 초기화
    outputs = net(trainX_tensor)  # 모델 예측
    loss = criterion(outputs, trainY_tensor)  # 손실 계산
    loss.backward()  # 역전파
    optimizer.step()  # 가중치 업데이트
    print(i, loss.item())  # 학습 진행 상황 출력

# 테스트 결과 시각화
plt.plot(testY)  # 실제 종가
plt.plot(net(testX_tensor).data.numpy())  # 예측된 종가
plt.legend(['original', 'prediction'])  # 범례 추가
plt.show()

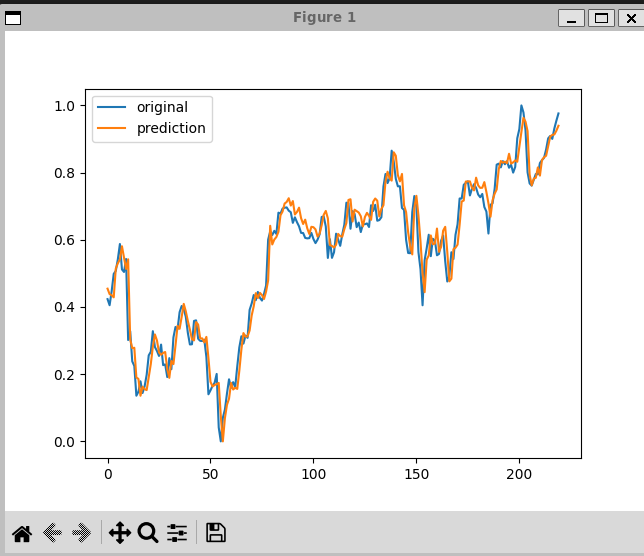
• 파란색 라인: 실제 테스트 데이터의 8일 차 종가
• 주황색 라인: 모델이 예측한 종가
• 두 라인이 거의 일치하여 모델이 예측을 잘 수행한다

Exercise

• 주식 시장의 변동성
  • 주식 시장은 외부 요인(뉴스, 정책 변화, 경제 상황 등)에 민감
  • 단순히 5개의 입력 데이터로 시장 전체를 예측하기는 어려움
• 추가적인 데이터
  • 뉴스나 트위터 데이터를 활용하여 키워드 감성을 분석하고 이를 모델에 넣는 방법도 있다
  • 다양한 피처를 추가하여 모델을 안정시키는 것이 중요